（九）信息融合方式简介

目录

前言

一、什么是信息融合？

二、集中式信息融合与分布式信息融合

（一）集中式融合

（二）分布式融合

1.简单信息融合

2.CI（协方差交叉）信息融合

3.无反馈的最优分布式融合

4.有反馈的最优分布式融合

三、仿真验证

（一）仿真设置

（二）仿真结果

总结

前言

        信息融合实质就是估计融合，即如何利用多个传感器的测量值所包含的信息，实现最优的状态估计。本文中的应用场景主要针对于多传感器目标跟踪中的航迹融合，融合结构可以分为集中式、分布式以及混合式。此处重点介绍集中式和分布式融合的概念，并且解释了跟踪过程中多传感器局部状态估计误差相关的原因。同时针对带反馈和不带反馈的分布式融合结构进行了仿真，实验结果证明两种结构形式下均能实现信息的有效融合，提升目标跟踪精度。（不同结构、不同滤波方式的信息融合代码均可以在资源中找到！）

一、什么是信息融合？

        信息融合就是利用多个传感器的信息提升状态估计精度的一种融合方式，其根本目的是减少冗余数据,提升数据的精度。目标跟踪过程中，主要是将来自不同传感器的航迹进行融合估计，以得到跟踪目标的实际运动状态。

        信息融合中误差相关的原因：

        1.共同的过程噪声：状态估计过程中信息来自于同一目标，虽然传感器的量测序列是独立的，但是由于目标的运动模型相同，具有共同的过程噪声Q，所以目标状态估计协方差是相关的。

        2.共同的先验信息：如果不同传感器滤波过程中有共同的先验信息，则传感器之间的局部误差是相关的。

二、集中式信息融合与分布式信息融合

        集中式信息融合和分布式信息融合的区别主要在于融合中心获取的信息形式不同。集中式融合中心接收到的信息是不同传感器传送的原始量测信息；分布式融合中心接收到的信息是不同传感器的状态估计值以及协方差矩阵，下文针对不同形式的信息融合方式进行详细的介绍。

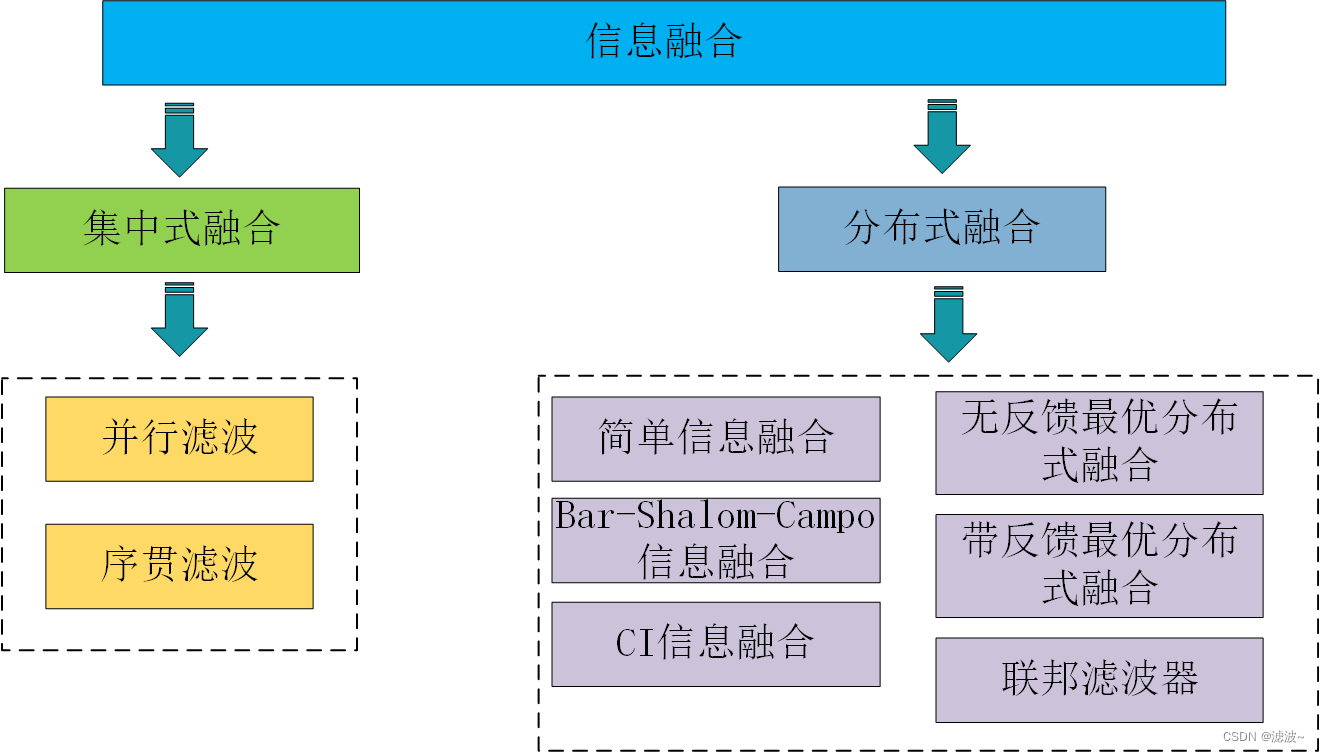
（一）集中式融合

        集中式信息融合为数据层的融合，就是将所有传感器的量测信息传送到融合中心进行数据处理，也称为“中心融合”或者“量测融合”。集中式信息融合可以利用所有传感器的原始测量信息进行融合，没有信息损失，得到的融合结果是最优的。但是这种结构需要很宽的数据链路来进行数据的传递，在工程上不容易实现。

（二）分布式融合

        分布式信息融合为状态层的融合，每个传感器独立对量测信息进行预处理，得到相应的状态估计值和局部协方差矩阵之后，再将信息传送到融合中心进行处理，得到全局状态估计值和全局协方差。这种方法也被称为“传感器级融合”或者“自主融合”，目标跟踪过程中也可称为“航迹融合”。由于此结构对于数据传输要求低，工程上容易实现，因此成为了信息融合领域的研究重点。针对分布式融合方式，仅介绍几种常用的融合方式。对其他结构感兴趣的同学可以自行翻找其他资料进行查阅。（具体的理论教材可以联系博主获取）

1.简单信息融合

        假设存在n个传感器。每个传感器的状态估计值为，误差协方差矩阵为,则对应的状态估计值和系统误差为：

        系统误差： 

        状态估计值：

2.CI（协方差交叉）信息融合

        假设存在n个传感器。每个传感器的状态估计值为，误差协方差矩阵为,则对应的状态估计值和系统误差为：

        系统误差： 

        状态估计值：

        权值：

3.无反馈的最优分布式融合

       假设存在n个传感器。每个传感器的状态估计值为，误差协方差矩阵为,则对应的状态估计值和系统误差为：

        全局和部分预测状态估计值和协方差为：

；

；

        系统误差： 

        状态估计值：

4.有反馈的最优分布式融合

         假设存在n个传感器。每个传感器的状态估计值为，误差协方差矩阵为,则对应的状态估计值和系统误差为： 

        反馈结构下满足以下条件：；

        系统误差：   

        状态估计值：                

三、仿真验证

（一）仿真设置

        假设在线性滤波条件下（非线性条件下需要计算雅可比行列式），雷达数量为；目标运动模型为CV模型；量测模型为线性；仿真步长为200帧；蒙特卡洛实验实验仿真次数为150次，具体参数设置见以下程序：

%参数设定
nd = 2;%2表示x和y这个二维平面；3表示x和y这个二维平面
np = 2;%2表示cv模型，有位置和速度两个量，3表示ca模型，有位置、速度和加速度三个量
nx = nd*np; %状态模型维数
nf = 0.1;%噪声强度
nz = 2;%测量维数
N_Q=1;%目标个数（简化目标产生函数）
N_R=2;%雷达个数
Ts = 1;
N_step = 200; %仿真时长
N_sim = 150;

radar_location=[-3e5 0;
                0 -3e5];

H = [1 0 0 0
     0 0 1 0];

ini_state(:,1) = [2000, 300, 1000, 100 ]';

R_base = [1000 0;
          0  1000]; %对应100000米时候的误差

        针对有反馈和无反馈结构的信息融合方式，其融合部分的代码结构不同。无反馈的信息融合部分代码为：

P_F_inv = 0;
X_f = 0;
X_1 = F*X_CI(:,i-1);
P_1 = F*P_CI{i-1}*F'+Q;
for j = 1:N_R
      P_F_inv = (eye(nx)/P{j,i}-(eye(nx)/(F*P{j,i-1}*F'+Q))) + P_F_inv ;
      X_f = ((eye(nx)/P{j,i}*x_filter{j,i})-(eye(nx)/(F*P{j,i-1}*F'+Q)*(F*x_filter{j,i-1}))) + X_f;
end

P_F_inv = P_F_inv+(eye(nx)/P_1);
P_CI{i} = eye(nx)/P_F_inv;
X_CI(:,i) =P_CI{i}*(eye(nx)/P_1*X_1+X_f);
RMSE_CI(1,i) = (X_CI(1,i)-X_real{1}(1,i))^2 + (X_CI(3,i)-X_real{1}(3,i))^2;

        有反馈的信息融合部分代码为：

P_F_inv = 0;    
X_f = 0;
X_1 = F*X_CI(:,i-1);
P_1 = F*P_CI{i-1}*F'+Q;

for j = 1:N_R
      P_F_inv = (eye(nx)/P{j,i}) + P_F_inv ;
      X_f = (eye(nx)/P{j,i})*(x_filter{j,i}-X_1) + X_f;
end

P_F_inv = P_F_inv-((N_R-1)*(eye(nx)/P_1));
P_CI{i} = eye(nx)/P_F_inv;
X_CI(:,i) = X_1 + P_CI{i}*X_f;
RMSE_CI(1,i) = (X_CI(1,i)-X_real{1}(1,i))^2 + (X_CI(3,i)-X_real{1}(3,i))^2;

（二）仿真结果

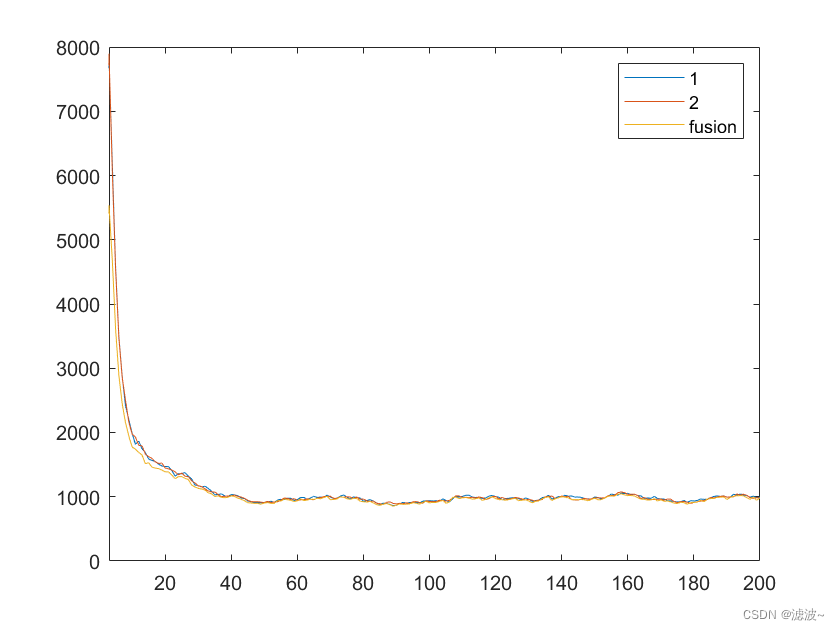
        上述两幅图为无反馈结构和反馈结构下的信息融合仿真结果图。第一幅图为无反馈条件下的信息融合仿真结果，从图中可以看出，信息融合方式有效提升了全局滤波精度，但是没有提升单个滤波器的跟踪精度。第二幅图为有反馈条件下的信息融合仿真结果，从图中可以看出，有无反馈的全局滤波精度相近，但是有反馈条件下的信息融合方式可以有效提升局部滤波的精度，并且便于滤波器的重新启动。

总结

        以上就是今天要讲的内容，本文简单介绍了现有的各种信息综合方式，给出了简单信息融合、CI信息融合、无反馈的最优分布式融合、有反馈的最优分布式融合的融合公式，同时针对线性量测、卡尔曼滤波、有无反馈条件下的分布式融合方法进行了仿真，仿真结果验证了信息融合方式可以有效提升滤波精度、并且反馈结构的信息融合方式可以提升局部滤波精度。（更多仿真见资源界面）