P问题，NP问题，NPC问题，NPH问题概念。’0/1背包判定问题是NPC问题‘和‘0/1背包问题是NPH问题但不是NPC问题’以及碰撞集是NPC问题‘证明。

2024-04-02 14:00:01
开发
20

概念

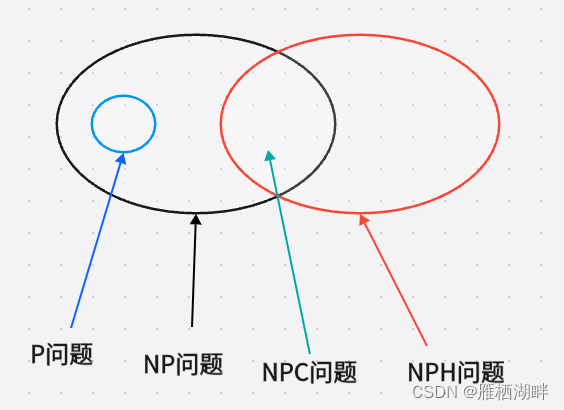
P问题：如果一个问题能找到在多项式时间内解决它的算法，那么该问题是P问题。

NP问题：如果可以在多项式时间内验证一个问题的解的正确性，那么该问题是NP问题。

NPC问题：一个NPC问题需要同时满足两个条件：（1）该问题是NP问题；（2）NP里所有问题可以在多项式时间内归约到该问题。

NPH问题：满足NPC中的条件（2）的问题，就是NPH问题。NPC问题是NPH问题的子集。

题1、0/1背包判定问题是NPC问题

题：已知带权集合的划分问题是 N PC 问题, 试证明 0/1 背包判定问题是 N PC 问题.

问题描述：例：给定一个有限集合 $X$ ，对每一个 $x\in X$ ，对应一个值 $w(x)\in Z^{+}$ ，和相应的值 $p(x)\in Z^{+}$ 。另外，还有一个容量约束 $M\in Z^{+}$ 和一个价值目标 $K\in Z^{+}$ 。

问：是否存在 $X$ 的一个子集 $X'$ ，使得 $\sum_{x\in X'}^{}w(x) \leq M$ ，而且 $\sum_{x\in X'}^{}p(x) \geq K$ 。

解答：

step1：证明0/1 背包判定问题是NP问题

给定集合 $X$ 的一个子集 $X'$ ，判定 $\sum_{x\in X'}^{}w(x) \leq M$ 并且 $\sum_{x\in X'}^{}p(x) \geq K$ ，仅需 $2*(|X'| - 1)$ 次的加法运算，其中 $|X'|$ 表示 $X'$ 的元素个数，时间复杂度是： $T(n) = O(|X'| - 1)$ ，即在多项式时间内完成判定，所以 $0/1$ 背包判定问题是NP问题。

step2：考虑特殊情况，令所有 $w(x) = p(x)$ ，并且取 $M=K=\frac{1}{2}\sum_{x\in X'}^{}w(x)$ 。这个 $0/1$ 背包判定问题回答“是”，当且仅当集合X划分问题回答“是”。已知划分问题为NPC问题，故0/1 背包判定问题是 N PC 问题。

题2、0/1背包问题是NPH问题

问题描述：有n个物品，它们有各自的体积 $w_{i}$ 和价值 $p_{i}$ ，现有给定容量M的背包，如何让背包里装入的物品具有最大的价值总和？

解答：

要得到 $max\sum_{i=1}^{n}x_{i}p_{i}$ $(s.t \sum_{i=1}^{n}x_{i}w_{i}\leq M)$ ，需要比较所有的 $X=(x_{1},x_{2},...,x_{n})$ ， $x_{i}\in$ $\left \{ 0,1 \right \}$ ，这有 $2^{n}$ 个可能，以比较为基础的求最大问题复杂度下界 $O(n)$ ，故本问题时间复杂度是 $O(2^{n})$ ，不存在多项式时间的算法，所以0/1背包问题不是NPC问题。

但0/1背包判定问题是NPC问题，0/1背包问题不比其更容易，所以，它是NPH问题。

题3：碰撞集（相遇集）是NPC问题证明。

问题描述：给一组集合 $\left \{ S_{1}, S_{2},..., S_{n} \right \}$ 和预算b，问是否存在一个集合 $H$ 满足 $|H|\leq b$ ，此集合和所有的 $S_{i}$ 相交为 $\varnothing$ ，其中 $|H|$ 是集合 $H$ 的元素个数。

解答：

step1：验证碰撞集为NP问题，只需要验证 $|H|\leq b$ ，且集合 $H$ 与任意 $S_{i}$ 相交不为 $\varnothing$ ，显然知时间复杂度为 $O(n|H||S|)$ ，在多项式时间内可以完成，故碰撞集是NP问题。

step2：已知顶点覆盖(vertex cover)问题是NPC问题，归约至目标问题：

(1)构建图G为碰撞集的映射：其中图G的每一个点对应碰撞集的每个元素，每条边对应 $S_{i}$ 。

(2)b个点的vertex cover 集对应规模大小为b的碰撞集：对于每一条边，至少有一个端点在b个点的vertex cover集中，所以这个集合和 $S_{i}$ 相交不为 $\varnothing$ ，此集合对应碰撞集。

(3)规模大小为b的碰撞集对应b个点的vertex cover集：任意的 $S_{i}$ 和碰撞集相交不为 $\varnothing$ ，则对应每条边支少有一个端点被选中，此碰撞集对应vertex cover 集。

综上所述，顶点覆盖问题可以归约到碰撞集，因此碰撞集也是NPC问题。

碰撞集问题借鉴

背包问题借鉴

原文地址:https://blog.csdn.net/2301_79707017/article/details/137230790 本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：https://www.suanlizi.com/kf/1775040469932314624.html 如若内容造成侵权/违法违规/事实不符，请联系《酸梨子》网邮箱：1419361763@qq.com进行投诉反馈，一经查实，立即删除！

阅读全部