1.为什么要学CNN
在传统神经网络中,我们要识别下图红色框中的图像时,我们很可能识别不出来,因为这六张图的位置都不通,计算机无法分辨出他们其实是一种形状或物体。
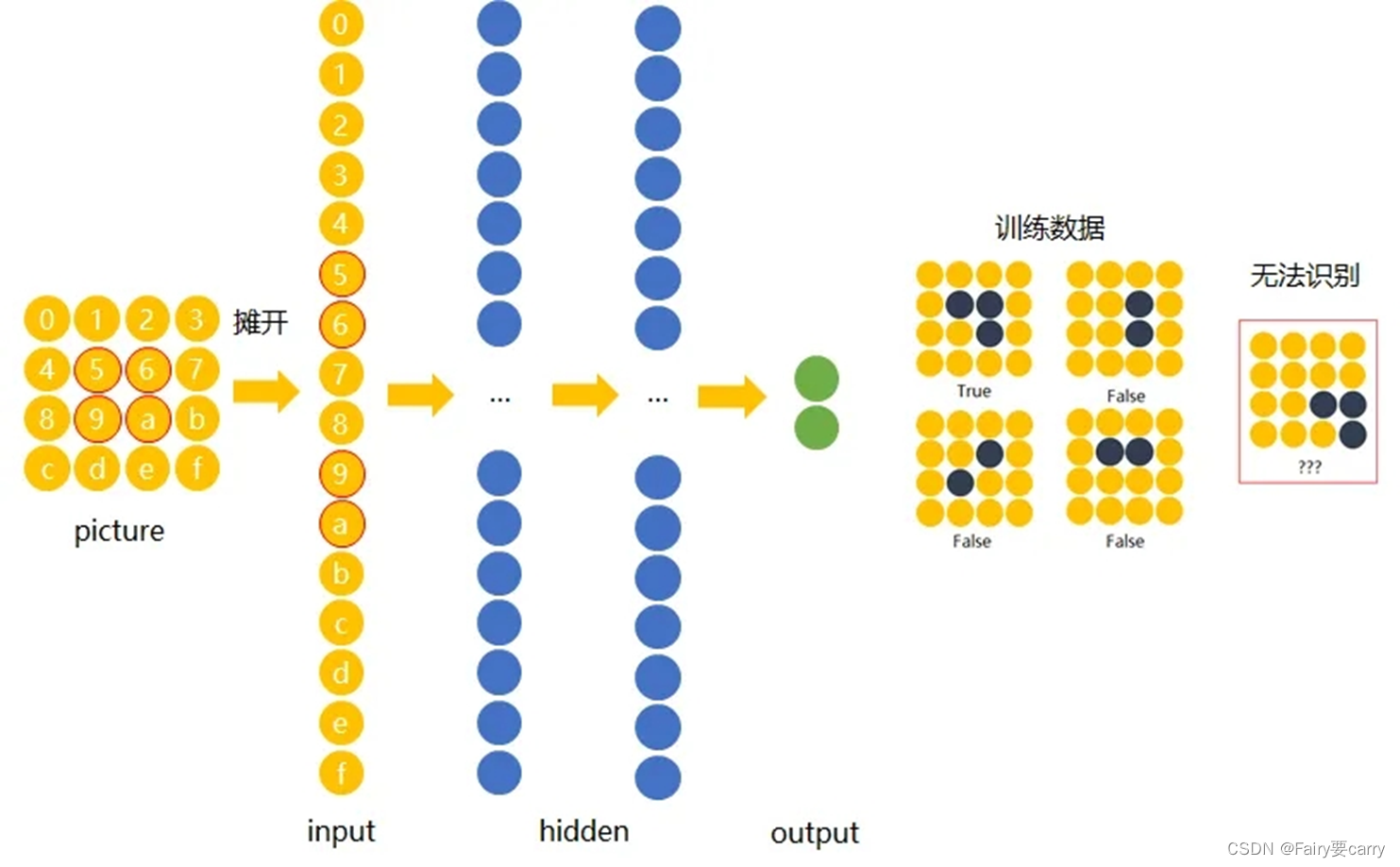
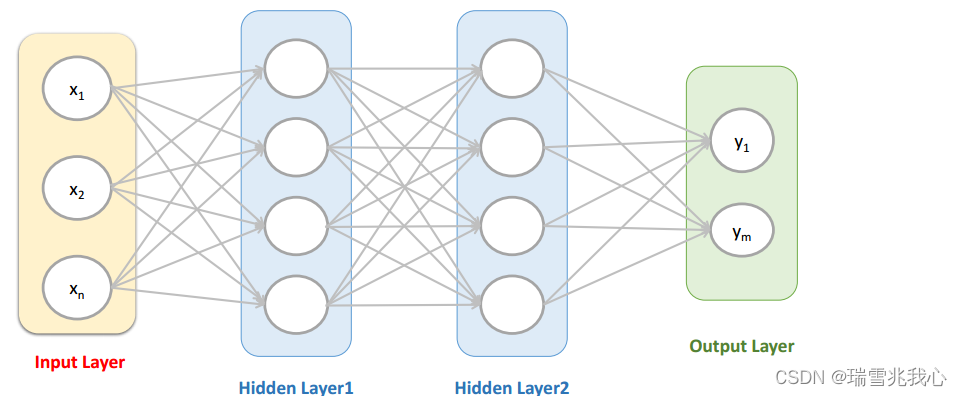
这是传统的神经网络图,通过权重调整神经元和神经元之间的关系达到处理信息的目的
另外,传统的神经网络在处理图像上有一些屏障:
**1.对于处理大图像和彩色图片有障碍:**目前用于计算机视觉问题的图像通常为224x224甚至更大,而如果处理彩色图片则又需加入3个颜色通道(RGB),即224x224x3。
如果构建一个BP神经网络,其要处理的像素点就有224x224x3=150528个,也就是需要处理150528个输入权重,而如果这个网络的隐藏层有1024个节点(这种网络中的典型隐藏层可能有1024个节点),那么,仅第一层隐含层我们就必须训练150528x1024=15亿个权重。这几乎是不可能完成训练的,更别说还有更大的图片了。
2.位置可变: 如果你训练了一个网络来检测狗,那么无论图像出现在哪张照片中,你都希望它能够检测到狗。
如果构建一个BP神经网络,则需要把输入的图片**“展平”(即把这个数组变成一列,然后输入神经网络进行训练)。但这破坏了图片的空间信息**。想象一下,训练一个在某个狗图像上运行良好的网络,然后为它提供相同图像的略微移位版本,此时的网络可能就会有完全不同的反应。
并且,有相关研究表明,人类大脑在理解图片信息的过程中,并不是同时观察整个图片,而是更倾向于观察部分特征,然后根据特征匹配、组合,最后得出整图信息。CNN用类似视觉的方式保留了图像的特征,当图像做翻转,旋转或者变换位置时,它也能有效的识别出来是类似的图像。
换句话说,在传统的ANN重,在BP全连接神经网络中,隐含层每一个神经元,都对输入图片 每个像素点 做出反应。这种机制包含了太多冗余连接。为了减少这些冗余,只需要每个隐含神经元,对图片的一小部分区域,做出反应就好了。而卷积神经网络,正是基于这种想法而实现的。
2.CNN卷积神经网络的特点
CNN是一种带有卷积结构的前馈神经网络,卷积结构可以减少深层网络占用的内存量,其中三个关键操作——局部感受野、权值共享、池化层,有效的减少了网络的参数个数,缓解了模型的过拟合问题。
卷积层和池化层一般会取若干个,采用卷积层和池化层交替设置,即一个卷积层连接一个池化层,池化层后再连接一个卷积层,依此类推。由于卷积层中输出特征图的每个神经元与其输入进行局部连接,并通过对应的连接权值与局部输入进行加权求和再加上偏置值,得到该神经元输入值,该过程等同于卷积过程,CNN也由此而得名。
与ANN(Artificial Neural Networks,人工神经网络)的区别:上一节所学习的MLP、BP,就是ANN。ANN通过调整内部神经元与神经元之间的权重关系,从而达到处理信息的目的。而在CNN中,其全连接层就是就是MLP,只不过在前面加入了卷积层和池化层。
3.CNN的主要结构
CNN主要包括以下结构:
**1、输入层(Input layer):**输入数据;
**2、卷积层(Convolution layer,CONV):**使用卷积核进行特征提取和特征映射;
**3、激活层:**非线性映射(ReLU)
**4、池化层(Pooling layer,POOL):**进行下采样降维;
**5、光栅化(Rasterization):**展开像素,与全连接层全连接,某些情况下这一层可以省去;
**6、全连接层(Affine layer / Fully Connected layer,FC):**在尾部进行拟合,减少特征信息的损失;
**7、激活层:**非线性映射(ReLU)
**8、输出层(Output layer):**输出结果。
其中,卷积层、激活层和池化层可叠加重复使用,这是CNN的核心结构。
在经过数次卷积和池化之后,最后会先将多维的数据进行“扁平化”,也就是把(height,width,channel)的数据压缩成长度为height × width × channel的一维数组,然后再与FC层连接,这之后就跟普通的神经网络无异了。(简而言之就是经过数次卷积操作和池化操作后,将我们的数据压缩为一维数组扁平化,后续操作和ANN差不多了)
3.1卷积层
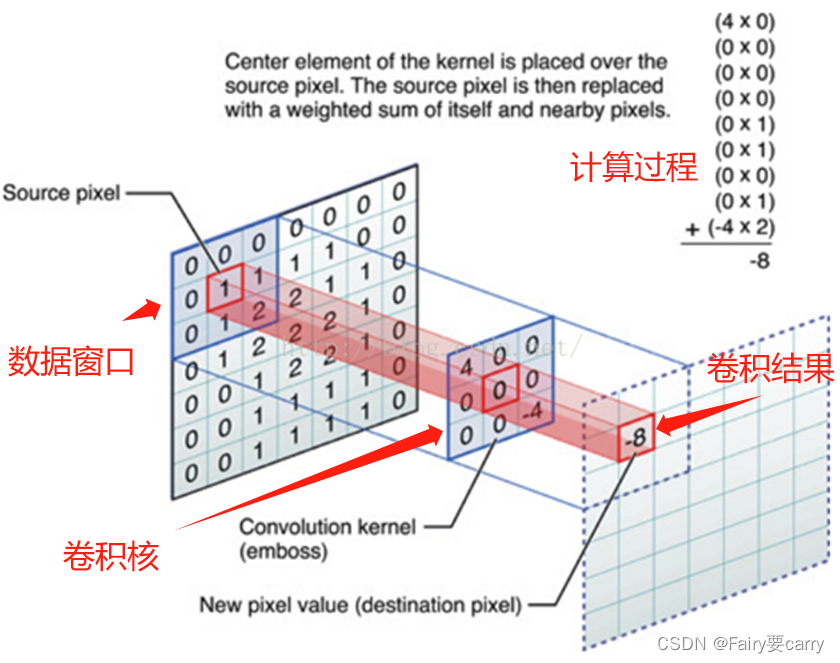
在卷积神经网络中,卷积操作是指将一个可移动的小窗口(称为数据窗口,如下图绿色矩形)与图像进行逐元素相乘然后相加的操作。这个小窗口其实是一组固定的权重,它可以被看作是一个特定的滤波器(filter)或卷积核。这个操作的名称“卷积”,源自于这种元素级相乘和求和的过程。这一操作是卷积神经网络名字的来源。
卷积层由一组滤波器组成,滤波器为三维结构,其深度由输入数据的深度决定,一个滤波器可以看作由多个卷积核堆叠形成。这些滤波器在输入数据上滑动做卷积运算,从输入数据中提取特征。在训练时,滤波器上的权重使用随机值进行初始化,并根据训练集进行学习,逐步优化。
3.1.1卷积运算和卷积核(Kernel)
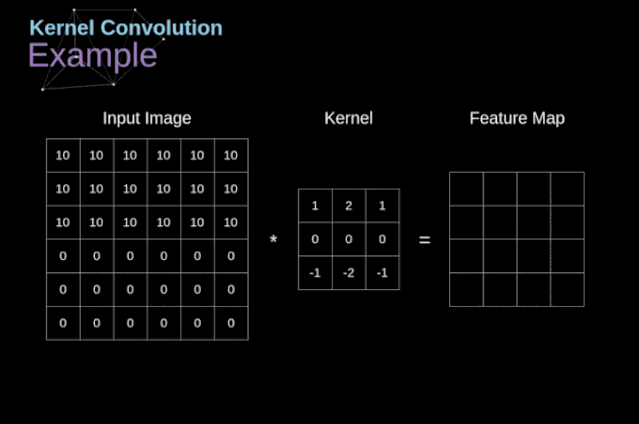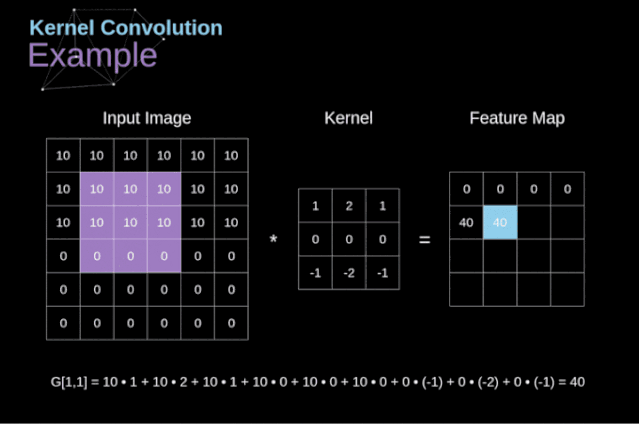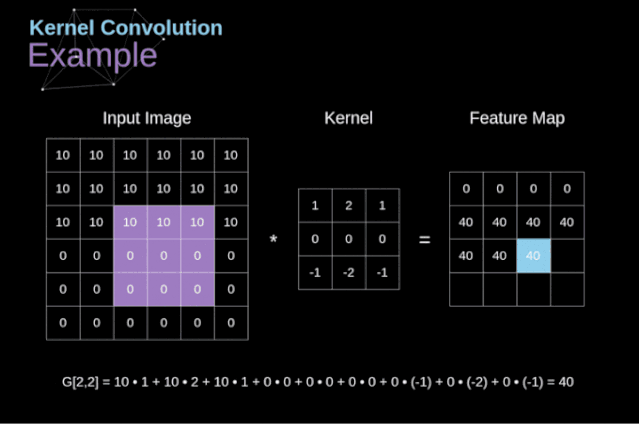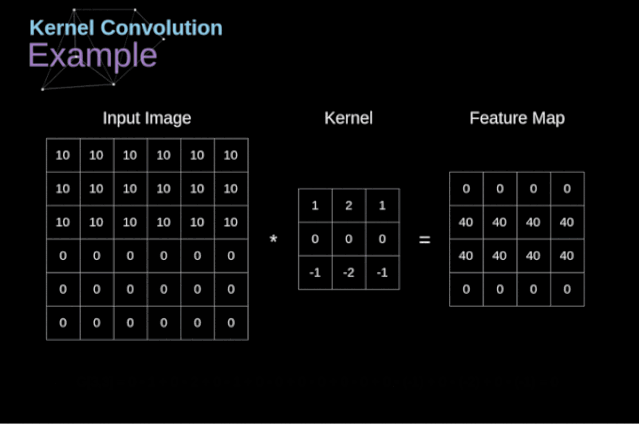

可以把卷积核理解为权重。每一个卷积核都可以当做一个**“特征提取算子”,把一个算子在原图上不断滑动,得出的滤波结果就被叫做“特征图”(Feature Map)**,这些算子被称为“卷积核”(Convolution Kernel)。我们不必人工设计这些算子,而是使用随机初始化,来得到很多卷积核,然后通过反向传播优化这些卷积核,以期望得到更好的识别结果。
3.2填充/填白(Padding)
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比如0等),使用填充的目的是调整输出的尺寸,使输出维度和输入维度一致;确保卷积核能够覆盖输入图像的边缘区域,同时保持输出特征图的大小。这对于在CNN中保留空间信息和有效处理图像边缘信息非常重要。
如果不调整尺寸,经过很多层卷积之后,输出尺寸会变的很小。所以,为了减少卷积操作导致的,边缘信息丢失,我们就需要进行填充(Padding)。目的就是:总长能被步长整除。
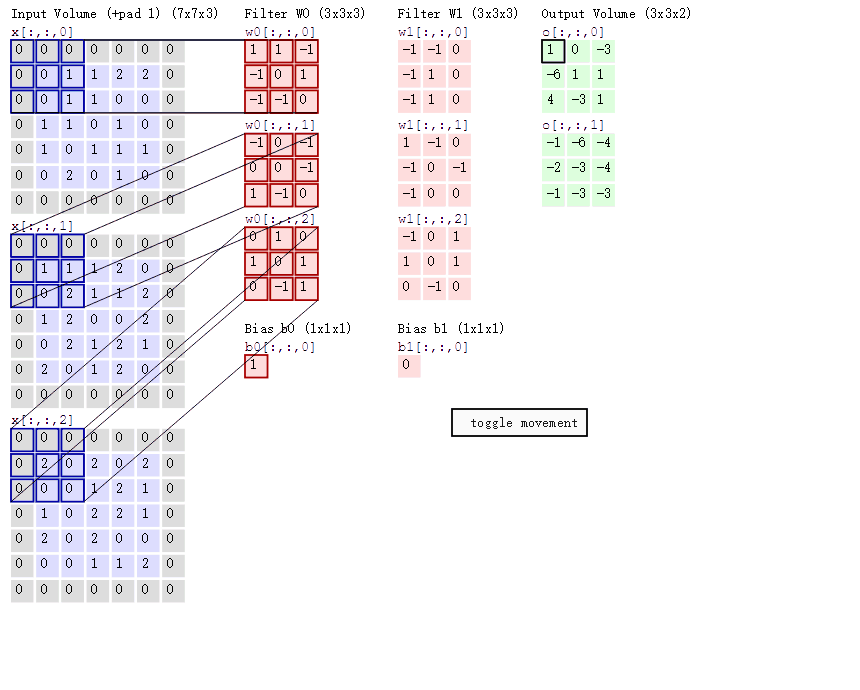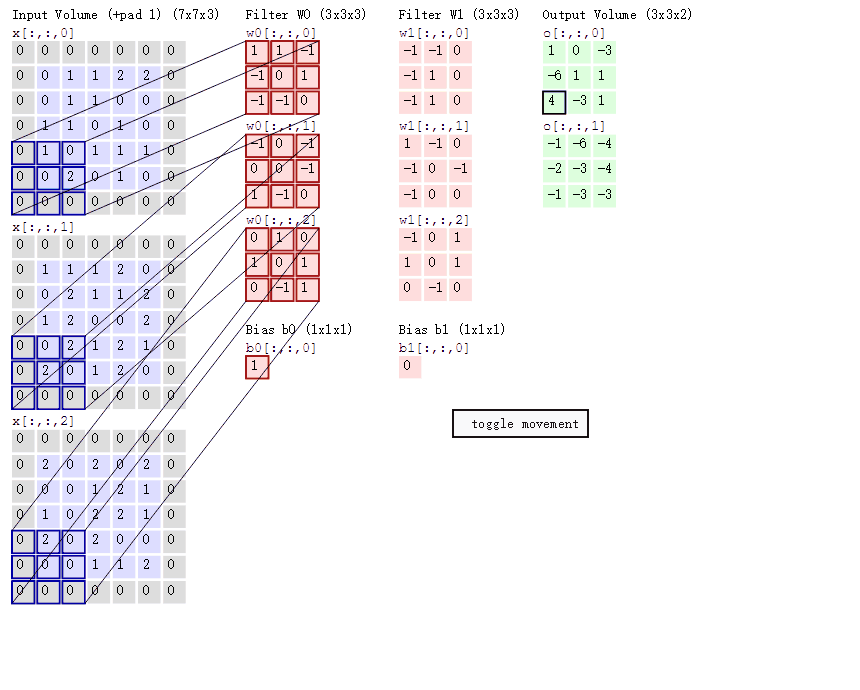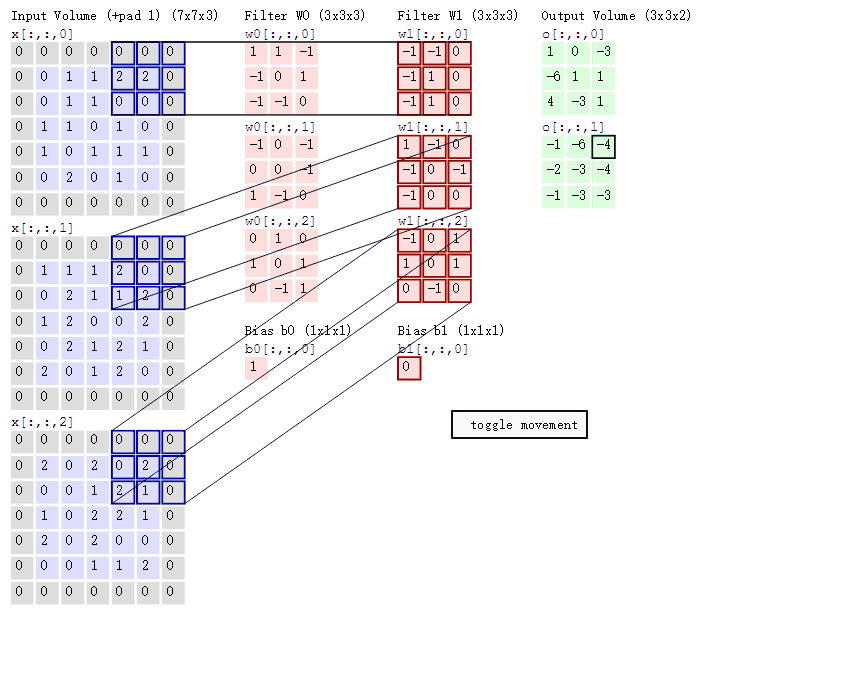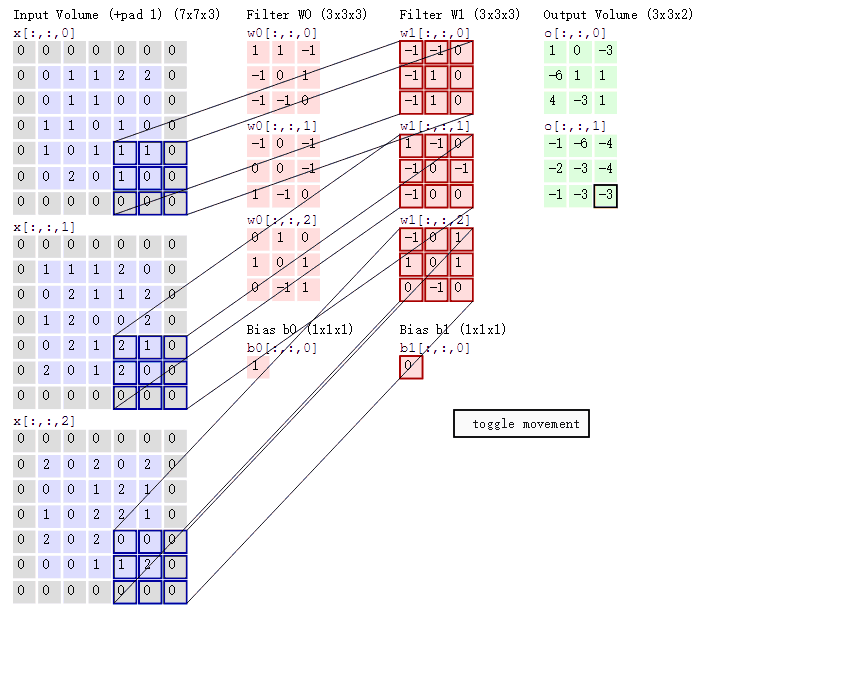
3.3在CNN中,卷积操作主要涉及以下几个步骤:
1.数据窗口和卷积核相乘:
首先,将一个称为卷积核(也称为滤波器)的小矩阵应用于输入数据的局部区域(数据窗口)。
对于每个数据窗口,将卷积核中的每个元素与对应的数据窗口中的元素相乘,然后将这些乘积相加,得到卷积结果的一个值。
2.步幅(Stride)和填充(Padding):
步幅定义了在应用卷积核时移动的步长,即每次移动的像素数。
填充是在输入数据周围添加额外像素值,以便在边缘处也能进行有效的卷积操作。
3.多个卷积核:
CNN通常会使用多个卷积核,每个卷积核可以捕获不同的特征,例如边缘、纹理等。
每个卷积核与输入数据进行卷积操作,生成对应的特征图(Feature Map)。
3.2 池化层(Pooling layer)
池化层通常出现在卷积层之后,二者相互交替出现,并且每个卷积层都与一个池化层一一对应。
1.作用: 用于缩小我们的尺寸和模型规模,提高运算速度,同时提高提取特征的鲁棒性(抗干扰能力),简单来说,就是为了提取一定区域的主要特征,并减少参数数量,减少了特征图的空间维度,有助于减少计算量并控制过拟合。,防止模型过拟合。
2.常见用法: 平均池化(Average Pooling / Mean Pooling)、最大池化(Max Pooling)、最小池化(Min Pooling)和随机池化(Stochastic Pooling)等,其中3种池化方式展示如下:
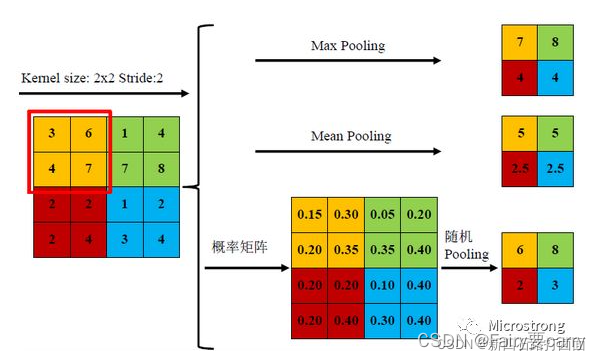
三种池化方式各有优缺点,均值池化是对所有特征点求平均值,而最大值池化是对特征点的求最大值。而随机池化则介于两者之间,通过对像素点按数值大小赋予概率,再按照概率进行亚采样,在平均意义上,与均值采样近似,在局部意义上,则服从最大值采样的准则。
根据Boureau理论2可以得出结论,在进行特征提取的过程中,均值池化可以减少邻域大小受限造成的估计值方差,但更多保留的是图像背景信息;而最大值池化能减少卷积层参数误差造成估计均值误差的偏移,能更多的保留纹理信息。随机池化虽然可以保留均值池化的信息,但是随机概率值确是人为添加的,随机概率的设置对结果影响较大,不可估计。
3.池化层的特征:
1、没有要学习的参数,这和池化层不同。池化只是从目标区域中取最大值或者平均值,所以没有必要有学习的参数。
2、通道数不发生改变,即不改变Feature Map的数量。
3、它是利用图像局部相关性的原理,对图像进行子抽样,这样对微小的位置变化具有鲁棒性——输入数据发生微小偏差时,池化仍会返回相同的结果。
3.3 全连接层
https://blog.csdn.net/weixin_57128596/article/details/138859784?spm=1001.2014.3001.5502
3.3.1步骤
1.稠密层

2.ReLU激活函数
作用:进行非线性增强网络的学习能力,加强特征


3.输出层(softmax函数激活)
通过softmax函数将输入进行归一化,转为概率分布(到底是属于哪一类)

4.例子
1、输入数据:
假设我们有一张大小为 28x28 像素的灰度图像作为输入数据。每个像素值表示像素的强度,范围从 0(黑色)到 255(白色)。
2、卷积层:
**滤波器/卷积核:**我们定义了几个滤波器(也称为卷积核),用于在输入图像上滑动。每个滤波器检测特定的特征,例如边缘或纹理。
**卷积操作:**对于每个滤波器,我们执行卷积操作,通过在输入图像上滑动滤波器,在每个位置计算滤波器与重叠区域的点积。
**激活函数:**在卷积操作之后,我们应用激活函数如 ReLU(修正线性单元),引入非线性并增强网络的学习能力。
卷积输出:卷积层的输出是一组特征图。每个特征图突出显示了由滤波器学习到的不同特征。
3、池化层:
池化操作:在池化层中,我们对每个特征图执行池化操作(通常是最大池化或平均池化)。池化减少了特征图的空间维度,有助于减少计算量并控制过拟合。
**池化大小:**通常,我们使用一个 2x2 像素的池化窗口,步长为 2,这意味着我们在每个 2x2 窗口内取最大或平均值,并每次移动窗口 2 个像素。
**池化输出:**池化层的输出是一组降采样的特征图,具有减小的空间维度。
4、展平:
在卷积和池化层之后,我们将前一层的输出展平为一个 1 维向量。这个展平步骤准备数据供全连接层使用。
5、全连接层:
**稠密层:**展平的向量输入一个或多个全连接(稠密)层。这些层中的每个神经元都与前一层中的每个神经元相连,允许网络学习复杂的模式。
**激活函数:**类似于卷积层,我们对每个稠密层的输出应用激活函数如 ReLU,非线性增强网络学习能力,保留主要信息特征。
**输出层:**最终的稠密层通常具有与分类任务中类别数相同的神经元数量(例如,在 MNIST 中有 10 个神经元用于数字识别)。
Softmax 激活:对于分类任务,我们通常在输出层使用 softmax 激活函数,将原始分数转换为概率。每个神经元的输出表示输入属于特定类别的概率。






















![[算法][数组][leetcode]2391. 收集垃圾的最少总时间](https://img-blog.csdnimg.cn/direct/8932a29edb094ee0af808b6e02045397.gif#pic_center)