编程奇境：C++之旅，从新手村到ACM/OI算法竞赛大门（武器：递归与递推）

上一期我们已经拿起了我们的第一把武器：排序算法，今天我们介绍第二把武器：递归与递推。

让我们用一个生活中的故事来形象地解释递归与递推这两个概念。

递归的故事：俄罗斯套娃

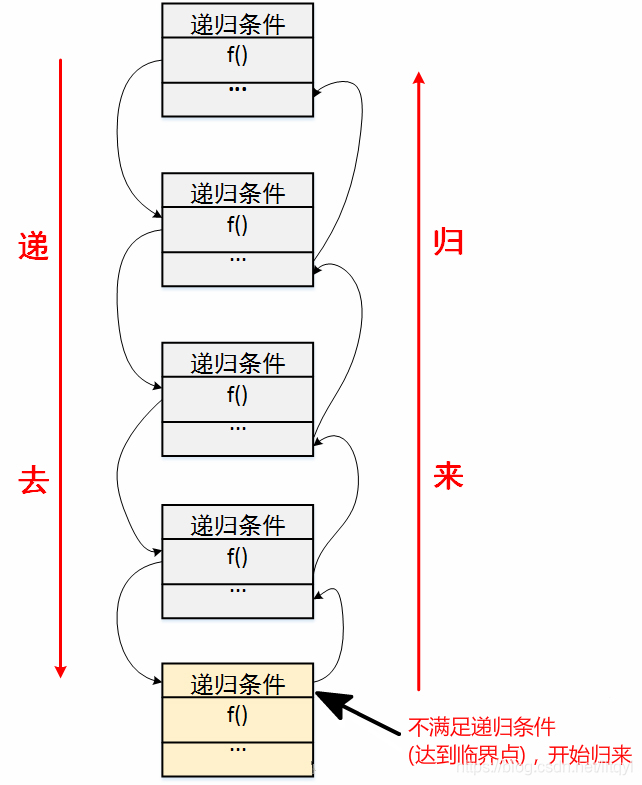
想象一下，你收到了一个精美的俄罗斯套娃作为礼物。这个套娃外面是一个大娃娃，当你打开它时，里面藏着一个稍小一点的套娃，再打开这个，又有一个更小的……如此类推，直到最后是一个最小的、无法再打开的小套娃。递归的概念就像是这个过程。每一个套娃在某种程度上都是一个自我复制的单元——它包含了另一个更小版本的自己。在编程中，递归函数就像这些套娃，它调用自己来解决问题，每次调用处理问题的一部分，直到遇到一个基本情况（最小的套娃），然后逐级返回结果。

递推的故事：登楼梯

递推则是另一种思维方式，想象你要爬上一段没有标楼层的楼梯，你不知道总共有多少阶，但你每次可以走一阶或两阶。为了知道到达顶层需要多少种不同的走法，你可以这样想：如果只有一阶，显然只有1种走法；如果有两阶，就有2种走法（1+1 或 2）。对于三阶，你可以从两阶的情况推算出来：到达第三阶，要么是从两阶处再走一阶上来，要么是从一阶处直接走两阶上来，所以总共有2+1=3种走法。继续这个逻辑，你可以推算出任何台阶数的走法。这就是递推，利用已知的较简单情况（如1阶和2阶）去推算更复杂情况（如3阶及以上）的解决方案，一步一步向上推理，直至达到你的目标。

递推

以登楼梯为例子，除了初始化的第一阶和第二阶，其他阶的方案数都可以由比他小的台阶推导出来，因为它要么是从前一级台阶上来的，要么是从前两级台阶上来的，所以我们就可以推出公式

f[i]=f[i-1]+f[i-2]

int f[5005];
int n;
int main()
{
	cin>>n;
	f[1]=1;
	f[2]=2;
	for(int i=3;i<=n;i++)
	{
		f[i]=f[i-1]+f[i-2];
	}
	cout<<f[n]<<endl;
	return 0;
}

这种由小状态推出大状态的思想就是递推。

递推在后序的动态规划中经常会出现。

练习题：

B2064 斐波那契数列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 

P1028 [NOIP2001 普及组] 数的计算 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

P1192 台阶问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

P2437 蜜蜂路线 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

P1025 [NOIP2001 提高组] 数的划分 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

递归 

想象一下，你有一堆书要从一楼搬到五楼，你可以这样搬：

1. 第一步：先拿起一本书，从一楼走到二楼。
2. 第二步：到了二楼，你其实面临一个新的任务——把剩下的书从二楼搬到三楼。这时候，你就可以像刚才一样，拿起一本书，走向三楼。
3. 第三步：每到新的一层，你就重复这个搬书的动作，直到所有书都被搬到五楼。

在这个过程中，每次你都是做着相同的事情（搬书上楼），只是楼层变了，这就是递归的思想。每次任务都像是上一次任务的缩小版，直到最后变成一个很简单的情况（比如只剩一本书，或者不需要再搬了）。

举个栗子，阶乘n!就是一种从大推到小的过程，因为n!=n*(n-1)*(n-2)*....*1。

阶乘是一个数和它以下所有正整数的乘积，记作n!。比如，5! = 5 × 4 × 3 × 2 × 1 = 120。

我们可以用递归的方式来想这个问题：

1. 如果n等于1，那么n!就等于1，这是最简单的情况，不需要再计算了。
2. 如果n大于1，比如n=5，那么5!就可以看成是5乘以(5-1)!，也就是5 × 4!。而4!又可以继续拆分，直到拆到1!为止。

我们可以写个函数来表示这个过程。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
int n;
int jc(int t)
{
	if(t==0)
	{
		return 1;
	}
	else
	{
		return t*jc(t-1);//递归调用 
	}
}
int main()
{
	cin>>n;
	cout<<jc(n)<<endl;
	return 0;
}

就像我们一层层地上楼梯，每次只关心怎么走下一步，递归就是让我们把大问题分解成一个个小问题，直到解决最简单的情况，然后答案自然就一层层“回传”回来了。 

这种由大状态推到小状态的过程就是递归。

递归在后续的DFS搜索和很多算法中是核心思想。

练习题 ：

P2089 烤鸡 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

先感受一下就好，后面慢慢用的多了就会懂一点。

总结

递归像是从上至下解决问题，不断地将大问题分解为包含自己的小问题，直到触及一个可以直接解答的基本情况。而递推则是从已知的基本情况出发，利用已知的结果去推导下一个或下几个层级的结果，一层一层往上构建答案。两者都是处理问题的有效手段，但递推通常避免了函数调用的开销，而递归在某些情况下提供了更为直观的解决方案表述。

百看不如一练，只有实践才是进步最快的方式，更要独立思考，如果想不出来了就看题解，会有眼前一亮的感觉。好啦，今天就到这里吧。下一期再见，记得给专栏点个关注，明天接着来哦~