完全背包
完全背包相对于01背包来说物品有无限个
代码的不同主要体现在遍历顺序上, 完全背包的背包重量不需要倒序遍历,因为物品有无限个,可以被无限添加;并且因为背包重量正序遍历,后续的值依赖于前面的值,因此背包和物品的内外层遍历也没有特定顺序
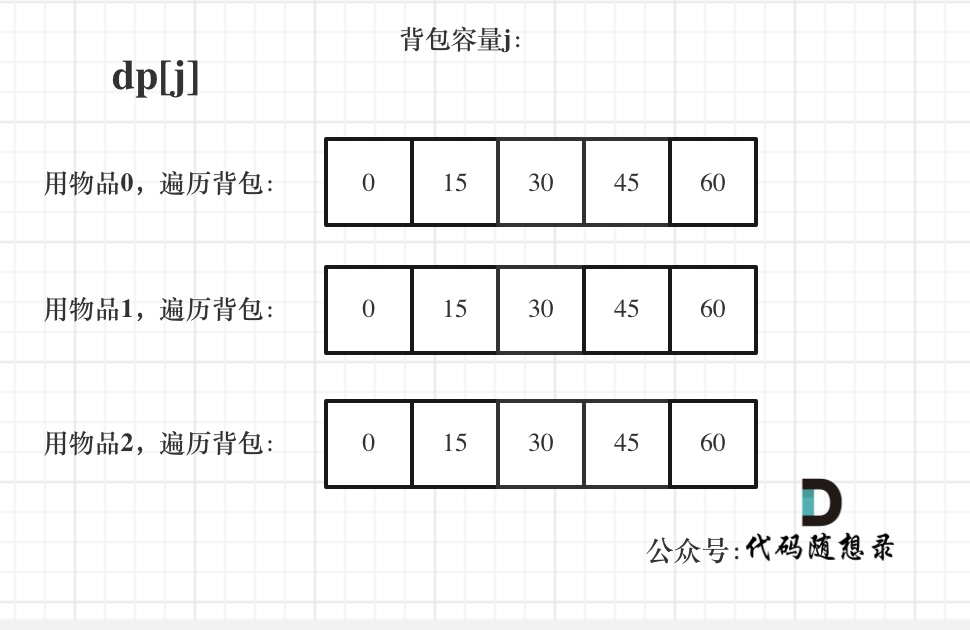
下面以物品外层循环,背包容量内层循环为例
def test_CompletePack(weight, value, bagWeight):
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(weight[i], bagWeight + 1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bagWeight]
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
result = test_CompletePack(weight, value, bagWeight)
print(result)518. 零钱兑换 II
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
动态规划五部曲:
- 确认dp数组以及下标的含义:dp[j]表示凑成金额j有dp[j]种不同的方式
- 确认递推公式:dp[j] += dp[j-weight[i]]
- dp数组的初始化:dp[0] = 1
- 确认遍历顺序:物品在外,背包容量在内正序遍历
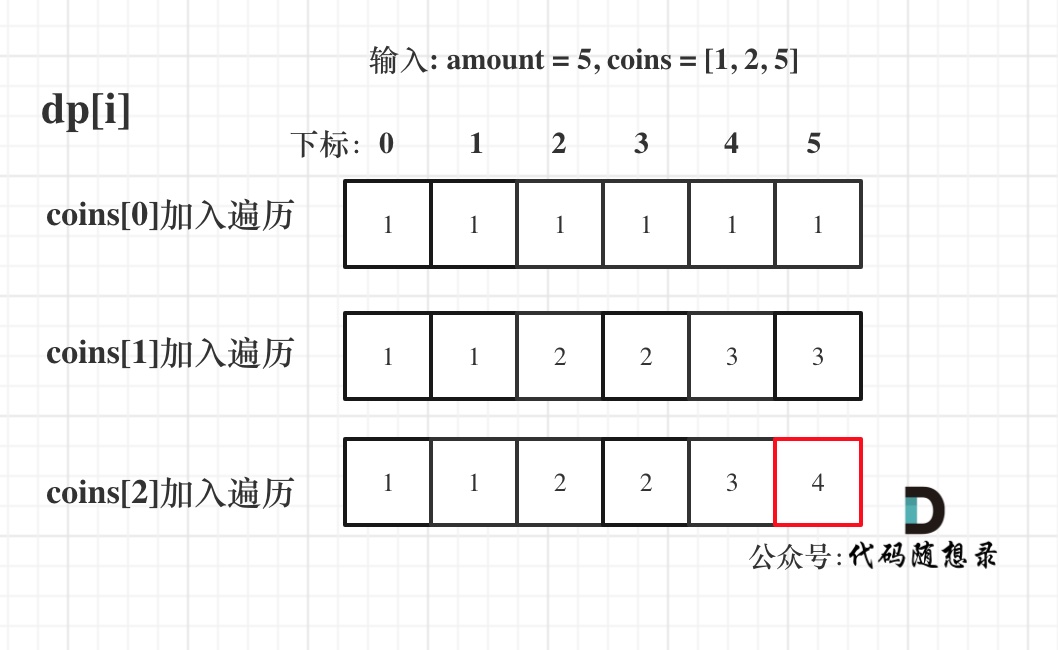
- 举例推导dp数组:
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0] * (amount+1)
dp[0] = 1
for coin in coins:
for j in range(coin, amount+1):
dp[j] += dp[j - coin]
return dp[amount]377. 组合总和 Ⅳ
- 确定dp数组以及下标的含义:dp[j]代表总和为j的排列个数为dp[j]
- 确定递推公式:dp[j] += dp[j-nums[i]]
- 数组的初始化:dp[0] = 1
- 确定遍历顺序:因为是求排列,不同顺序算不同结果,因此背包重量在外层循环,物品在内层循环
- 举例推导dp数组:
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1)
dp[0] = 1
for j in range(target + 1):
for num in nums:
if j >= num:
dp[j] += dp[j-num]
return dp[target]