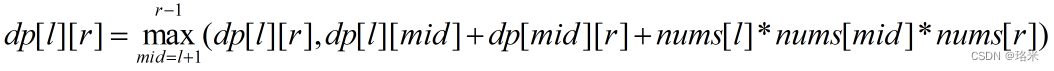【C语言】Leetcode-312 戳气球

题目

链接: Leetcode-312 戳气球

思路

我们观察戳气球的操作，发现这会导致两个气球从不相邻变成相邻，使得后续操作难以处理。于是我们倒过来看这些操作，将全过程看作是每次添加一个气球。

首先
我们需要创建一个 $val$ 数组，用来存储所有的元素，其中 $val[0]$ 和 $val[numsSize+1]$ 的位置用来存放两头的超出数组边界的1，剩下的从1开始就是 $nums$ 数组里的元素

然后
我们定义 $solve$ 方法，令 $slove(i,j)$ 表示开区间 $(i,j)$ 内的位置全部填满气球能够得到的最多硬币数。由于时开区间，因此区间两端的气球编号就是 $val[i[$ 和 $val[j]$

接着
我们要对这个 $slove$ 方法进行分类讨论

当 $i>=j-1$ 时，开区间中没有气球，$slove(i,j)$ 的值为0

当 $i<j-1$ 时，我们美剧开区间 $(i,j)$ 内的全部位置 $mid$ ，令 $mid$ 为当前区间第一个添加的气球，该操作能得到的硬币数为 $val[i]\ast val[mid]\ast val[j]$

同时我们利用递归，去计算分割出的两区间对 $solve(i,j)$ 的贡献，这三项之和的最大值，即为 $solve(i,j)$ 的值

还有
因为我们是利用递归将每种结果都计算出来，所以他的工程量是很大的，为了降低时间复杂度，我们可以建立一个二维数组，来根据 $left$ 和 $right$ 的值存放这个开区间内的最大贡献量

代码如下

int rec[302][302];
int val[302];

int solve(int left, int right) {
    if (left >= right - 1)
        return 0;
    if (rec[left][right] != -1)
        return rec[left][right];
    for (int i = left + 1; i < right; i++) {
        int sum = val[left] * val[i] * val[right];
        sum += solve(left, i) + solve(i, right);
        rec[left][right] = fmax(rec[left][right], sum);
    }
    return rec[left][right];
}

int maxCoins(int* nums, int numsSize) {
    memset(rec, -1, sizeof(rec));
    val[0] = val[numsSize + 1] = 1;
    for (int i = 1; i <= numsSize; i++) {
        val[i] = nums[i - 1];
    }
    return solve(0, numsSize + 1);
}