图论
图的基本概念
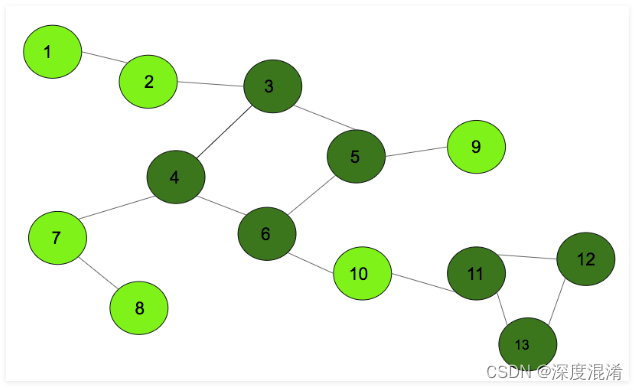
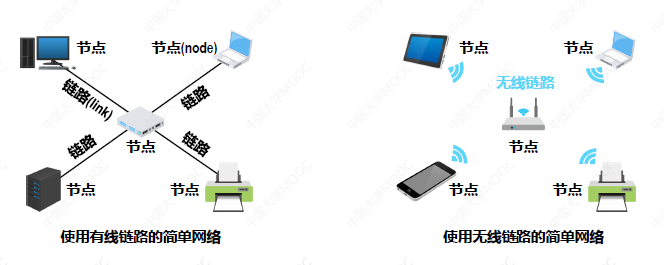
图是由很多结点和边组成的

点的表示:v,点的集合:V
边的表示:e,边的集合:E
图:G = (V,E)
无向图和有向图
无向图:边没有方向
有向图:边有方向
无权图和有权图
无权图:所有边的权重都是一样的,都等于1
有权图:边有权重,权重的大小各不相同
权重的物理意义:可以是距离、长度、宽度等
不存在的边可以是权重无穷大、权重为0的边
图的数据结构
无向无权图
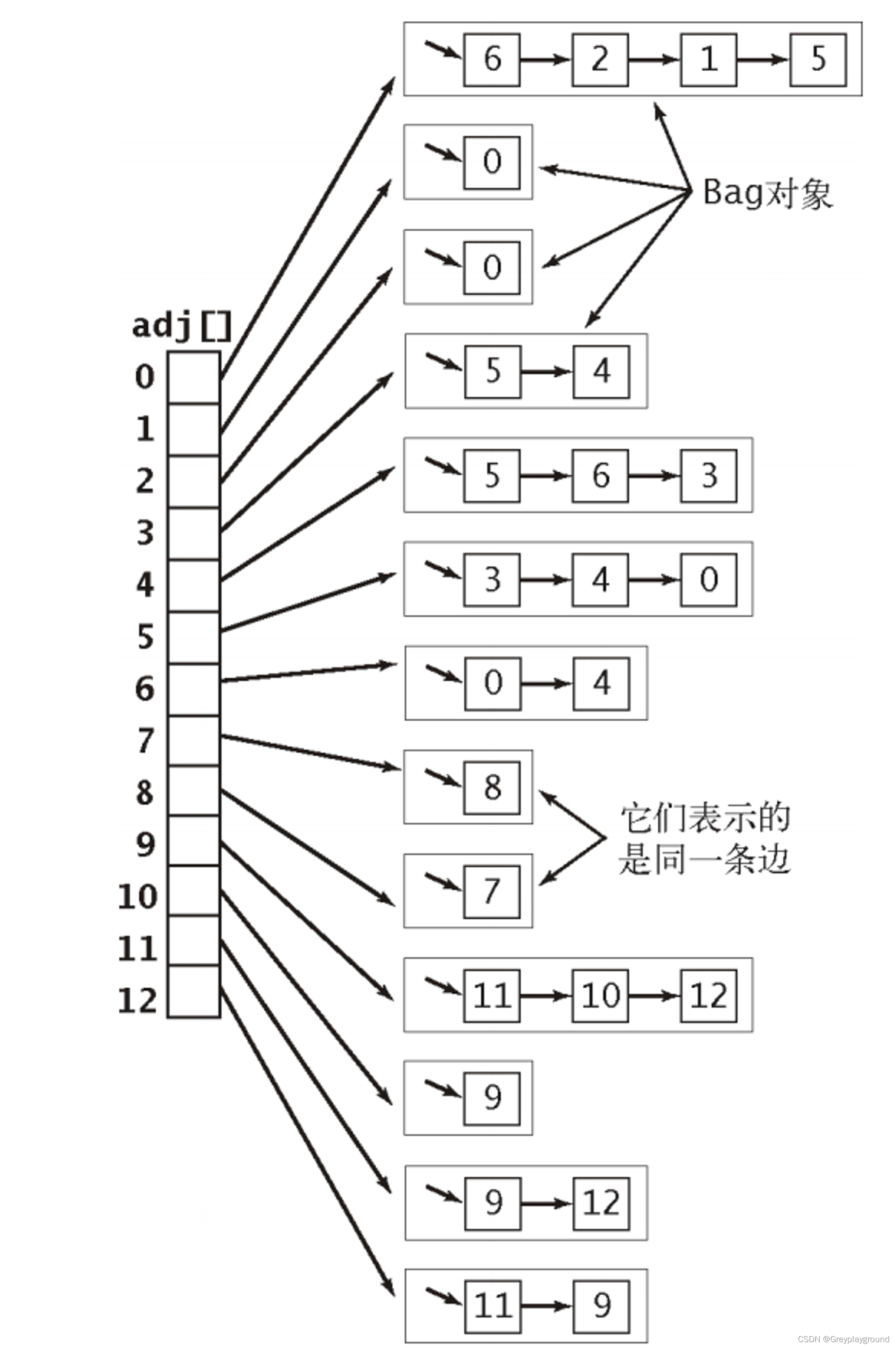
邻接表

邻接矩阵

一条边对应邻接矩阵的两个元素
邻接矩阵是对称的
有向无权图
邻接表
邻接矩阵
行为To,列为From
一条边对应邻接矩阵的一个元素
邻接矩阵通常是对称的
无向有权图
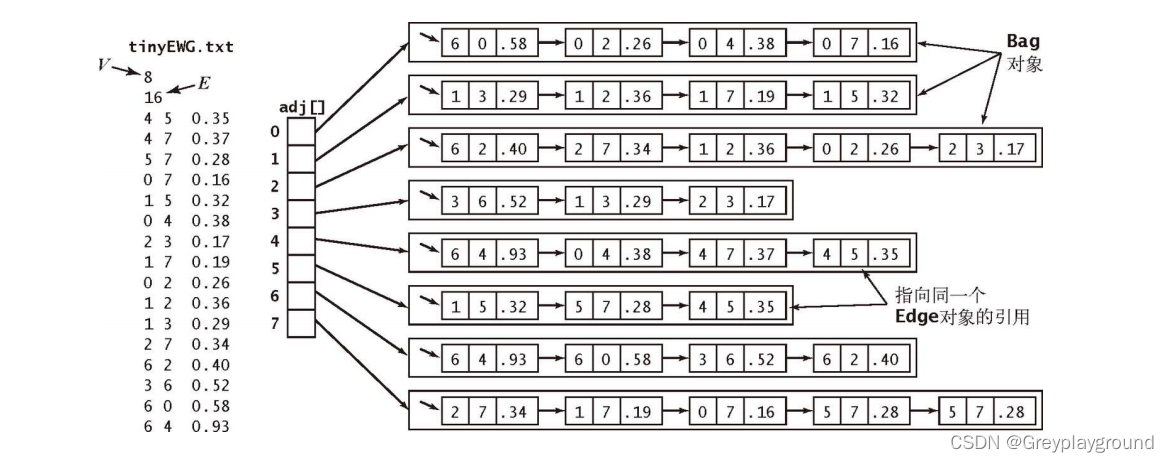
邻接矩阵
一条边对应邻接矩阵的两个元素
邻接矩阵是对称的
有向有权图
邻接矩阵
一条边对应邻接矩阵的一个元素
邻接矩阵通常是非对称的
最短路问题
概念
路径:可以表示为结点的序列或边的序列
简单路径的概念:路径上没有重复结点
路径不存在:路径的长度为正无穷
无权图路径的长度 = 路径边数
有权图路径的长度 = 路径边权重总和
最短路问题:
输入图和起点s,输出s到其它所有结点的最短路径
记录到每个结点的最短路径、前一个结点
算法:寻找无权图中的最短路
以有向图为例,同样适用于无向图
空队列、表(bool是否访问过该节点, int路径长度, path前一个结点)