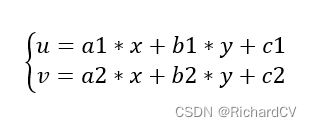多元散射校正预处理方法原理公式及python实现代码

多元散射校正（MSC，Multiplicative Scatter Correction）是一种用于光谱数据预处理的技术，主要用于消除由于散射效应和颗粒大小差异引起的光谱基线漂移和幅度变化。

MSC的主要目标是将测量的光谱校正到一个基准光谱上，从而减少这些不相关的变化。基准光谱通常是所有测量光谱的平均光谱。选择平均光谱作为参考光谱可以很好地代表整个数据集的特征。

MSC的公式如下：

① 计算所有光谱数据的均值作为基准光谱：

② 对每个测量光谱进行线性回归：

对于每个测量光谱X，用最小二乘法拟合一个线性模型：

③ 计算校正后的光谱：

使用得到的a和b校正原始光谱：

注：其中a和b的计算方法如下：

a. 计算均值：计算每个测量光谱X的均值和基准光谱的均值

b. 计算测量光谱和基准光谱之间的协方差：

c. 计算基准光谱的方差：

d: 计算回归系数a和b：

具体示例

假设有一个基准光谱和一个测量光谱 ，它们在某些波长点上的值如下：

我们计算均值： 

计算协方差和方差：

计算回归系数：

最后，计算校正后的光谱：

python代码实现（使用LinearRegression函数和手动实现的两种方式）：

def msc(X):
    """
    Perform Multiplicative Scatter Correction (MSC) on the given spectral data.
    
    Parameters:
    X (ndarray): The input spectral data matrix, where rows are samples and columns are wavelengths.
    
    Returns:
    ndarray: The MSC corrected spectral data.
    """
    # Calculate the mean spectrum
    X_ref = np.mean(X, axis=0)
    
    # Initialize the corrected spectra matrix
    X_msc = np.zeros_like(X)
    
    # Perform MSC on each spectrum
    for i in range(X.shape[0]):
        # Reshape data for LinearRegression
        X_ref_reshaped = X_ref.reshape(-1, 1)
        X_i_reshaped = X[i].reshape(-1, 1)
        
        # Fit linear regression model
        model = LinearRegression().fit(X_ref_reshaped, X_i_reshaped)
        a = model.coef_[0][0]
        b = model.intercept_[0]
        
        # Apply correction
        X_msc[i] = (X[i] - b) / a
    
    return X_msc

import numpy as np
import matplotlib.pyplot as plt

def msc_manual(X):
    """
    Perform Multiplicative Scatter Correction (MSC) on the given spectral data manually.
    
    Parameters:
    X (ndarray): The input spectral data matrix, where rows are samples and columns are wavelengths.
    
    Returns:
    ndarray: The MSC corrected spectral data.
    """
    # Calculate the mean spectrum
    X_ref = np.mean(X, axis=0)
    
    # Initialize the corrected spectra matrix
    X_msc = np.zeros_like(X)
    
    # Perform MSC on each spectrum
    for i in range(X.shape[0]):
        # Calculate means
        X_i = X[i]
        mean_X_i = np.mean(X_i)
        mean_X_ref = np.mean(X_ref)
        
        # Calculate covariance and variance
        covariance = np.mean((X_i - mean_X_i) * (X_ref - mean_X_ref))
        variance = np.mean((X_ref - mean_X_ref) ** 2)
        
        # Calculate regression coefficients
        a = covariance / variance
        b = mean_X_i - a * mean_X_ref
        
        # Apply correction
        X_msc[i] = (X_i - b) / a
    
    return X_msc