图论之岛屿系列
形成模板进行学习,加快学习效率
深度优先遍历
# 可以直接改原始grid的采用直接改的方案来完成修改,减少了内存开支
def dfs(self, grid, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == "0": # 过滤条件
return
grid[i][j] = "0" # 写变换条件
self.dfs(grid, i - 1, j)
self.dfs(grid, i + 1, j)
self.dfs(grid, i, j - 1)
self.dfs(grid, i, j + 1)
return
# 无法改原始grid,需要visible辅助
def dfs(self, grid, visible, i, j):
if (
i < 0
or j < 0
or i >= len(grid)
or j >= len(grid[0])
or grid[i][j] == "0"
or visible[i][j]
):
return
visible[i][j] = True
self.dfs(grid, visible, i - 1, j)
self.dfs(grid, visible, i + 1, j)
self.dfs(grid, visible, i, j - 1)
self.dfs(grid, visible, i, j + 1)
return
广度优先遍历
# 原有grid进行处理
def bfs(self, grid, i, j):
queue = deque([[i, j]])
grid[i][j] = "0"
while queue:
cur_x, cur_y = queue.pop()
if cur_x - 1 >= 0 and grid[cur_x - 1][cur_y] == "1":
queue.append([cur_x - 1, cur_y])
grid[cur_x - 1][cur_y] = "0"
if cur_x + 1 < len(grid) and grid[cur_x + 1][cur_y] == "1":
queue.append([cur_x + 1, cur_y])
grid[cur_x + 1][cur_y] = "0"
if cur_y - 1 >= 0 and grid[cur_x][cur_y - 1] == "1":
queue.append([cur_x, cur_y - 1])
grid[cur_x][cur_y - 1] = "0"
if cur_y + 1 < len(grid[0]) and grid[cur_x][cur_y + 1] == "1":
queue.append([cur_x, cur_y + 1])
grid[cur_x][cur_y + 1] = "0"
return
# 提供辅助visible进行处理
def bfs(self, grid, nums, i, j):
queue = deque([[i, j]])
nums.add((i, j))
while queue:
cur_x, cur_y = queue.pop()
if (
cur_x - 1 >= 0
and grid[cur_x - 1][cur_y] >= grid[cur_x][cur_y]
and (cur_x - 1, cur_y) not in nums
):
queue.append([cur_x - 1, cur_y])
nums.add((cur_x - 1, cur_y))
if (
cur_x + 1 < len(grid)
and grid[cur_x + 1][cur_y] >= grid[cur_x][cur_y]
and (cur_x + 1, cur_y) not in nums
):
queue.append([cur_x + 1, cur_y])
nums.add((cur_x + 1, cur_y))
if (
cur_y - 1 >= 0
and grid[cur_x][cur_y - 1] >= grid[cur_x][cur_y]
and (cur_x, cur_y - 1) not in nums
):
queue.append([cur_x, cur_y - 1])
nums.add((cur_x, cur_y - 1))
if (
cur_y + 1 < len(grid[0])
and grid[cur_x][cur_y + 1] >= grid[cur_x][cur_y]
and (cur_x, cur_y + 1) not in nums
):
queue.append([cur_x, cur_y + 1])
nums.add((cur_x, cur_y + 1))
return
实例
岛屿数量题目描述:
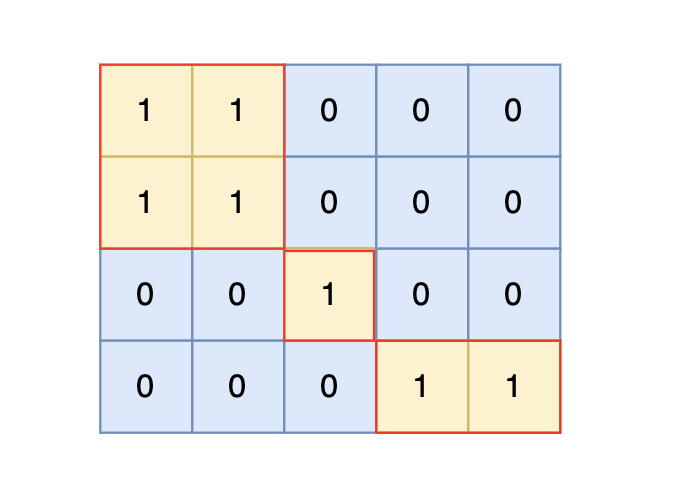
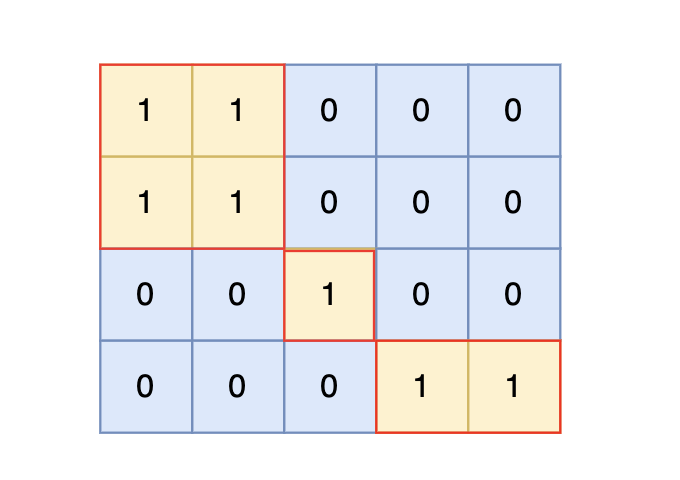
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述:
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
3
实现方案
将遍历过的grid设置为0
- 深度优先遍历
class Solution:
def dfs(self, grid, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == "0":
return
grid[i][j] = "0"
self.dfs(grid, i - 1, j)
self.dfs(grid, i + 1, j)
self.dfs(grid, i, j - 1)
self.dfs(grid, i, j + 1)
return
def numIslands(self, grid: List[List[str]]) -> int:
m, n = len(grid), len(grid[0])
cnt = 0
for i, j in product(range(m), range(n)):
if grid[i][j] == "1":
self.dfs(grid, i, j)
cnt += 1
return cnt
- 广度优先遍历
class Solution:
def bfs(self, grid, i, j):
queue = deque([[i, j]])
grid[i][j] = "0"
while queue:
cur_x, cur_y = queue.pop()
if cur_x - 1 >= 0 and grid[cur_x - 1][cur_y] == "1":
queue.append([cur_x - 1, cur_y])
grid[cur_x - 1][cur_y] = "0"
if cur_x + 1 < len(grid) and grid[cur_x + 1][cur_y] == "1":
queue.append([cur_x + 1, cur_y])
grid[cur_x + 1][cur_y] = "0"
if cur_y - 1 >= 0 and grid[cur_x][cur_y - 1] == "1":
queue.append([cur_x, cur_y - 1])
grid[cur_x][cur_y - 1] = "0"
if cur_y + 1 < len(grid[0]) and grid[cur_x][cur_y + 1] == "1":
queue.append([cur_x, cur_y + 1])
grid[cur_x][cur_y + 1] = "0"
return
def numIslands(self, grid: List[List[str]]) -> int:
m, n = len(grid), len(grid[0])
cnt = 0
for i, j in product(range(m), range(n)):
if grid[i][j] == "1":
self.bfs(grid, i, j)
cnt += 1
return cnt
岛屿的最大面积
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。后续 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的最大面积。如果不存在岛屿,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
4
提示信息
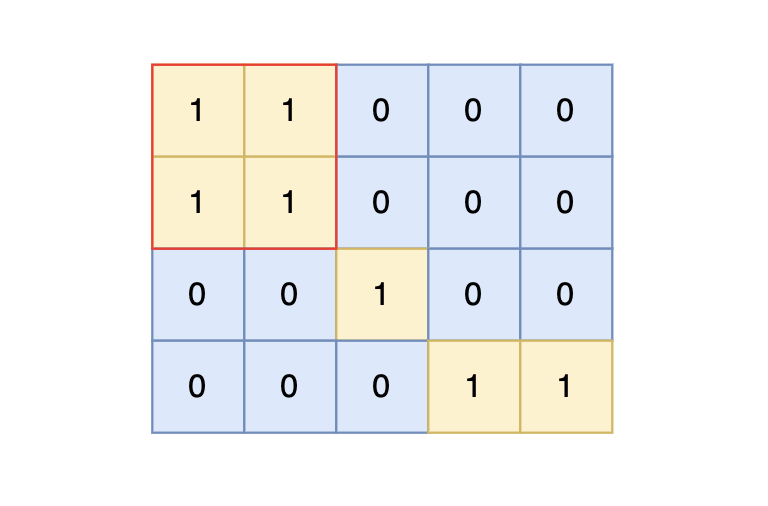
样例输入中,岛屿的最大面积为 4。
数据范围:
方案:
与岛屿数量一致,增加一个计数功能即可
- 深度优先遍历
class Solution:
def dfs(self, grid, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == 0:
return
self.cnt += 1
grid[i][j] = 0
self.dfs(grid, i - 1, j)
self.dfs(grid, i + 1, j)
self.dfs(grid, i, j - 1)
self.dfs(grid, i, j + 1)
return
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
maxN = 0
m, n = len(grid), len(grid[0])
for i, j in product(range(m), range(n)):
if grid[i][j] == 1:
self.cnt = 0
self.dfs(grid, i, j)
maxN = max(maxN, self.cnt)
return maxN
- 广度优先遍历
class Solution:
def bfs(self, grid, i, j):
queue = deque([[i, j]])
grid[i][j] = 0
cnt = 1
while queue:
cur_x, cur_y = queue.pop()
if cur_x - 1 >= 0 and grid[cur_x - 1][cur_y] == 1:
queue.append([cur_x - 1, cur_y])
grid[cur_x - 1][cur_y] = 0
cnt += 1
if cur_x + 1 < len(grid) and grid[cur_x + 1][cur_y] == 1:
queue.append([cur_x + 1, cur_y])
grid[cur_x + 1][cur_y] = 0
cnt += 1
if cur_y - 1 >= 0 and grid[cur_x][cur_y - 1] == 1:
queue.append([cur_x, cur_y - 1])
grid[cur_x][cur_y - 1] = 0
cnt += 1
if cur_y + 1 < len(grid[0]) and grid[cur_x][cur_y + 1] == 1:
queue.append([cur_x, cur_y + 1])
grid[cur_x][cur_y + 1] = 0
cnt += 1
return cnt
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
maxN = 0
m, n = len(grid), len(grid[0])
for i, j in product(range(m), range(n)):
if grid[i][j] == 1:
cnt = self.bfs(grid, i, j)
maxN = max(maxN, cnt)
return maxN
孤岛的总面积
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例:
1
提示信息:

解题思路:
反方向法,求孤岛,只需要把不是孤岛的给变成海即可,剩下的都是孤岛,不是孤岛的需要从上下左右边界进行海化
- 深度优先遍历
class Solution:
def dfs(self, grid, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or grid[i][j] == 0:
return
grid[i][j] = 0
self.dfs(grid, i - 1, j)
self.dfs(grid, i + 1, j)
self.dfs(grid, i, j - 1)
self.dfs(grid, i, j + 1)
def SumAreaIsolatedLand(self, grid):
m, n = len(grid), len(grid[0])
sumN = 0
for j in [0, -1]:
for i in range(m):
if grid[i][j] == 1:
self.dfs(grid, i, j)
for i in [0, -1]:
for j in range(1, n - 1):
if grid[i][j] == 1:
self.dfs(grid, i, j)
for i, j in product(range(1, m - 1), range(1, n - 1)):
if grid[i][j] == 1:
sumN += 1
return sumN
- 广度优先遍历
class Solution:
def bfs(self, grid, i, j):
queue = deque([[i, j]])
grid[i][j] = 0
while queue:
cur_x, cur_y = queue.pop()
if cur_x - 1 >= 0 and grid[cur_x - 1][cur_y] == 1:
queue.append([cur_x - 1, cur_y])
grid[cur_x - 1][cur_y] = 0
if cur_x + 1 < len(grid) and grid[cur_x + 1][cur_y] == 1:
queue.append([cur_x + 1, cur_y])
grid[cur_x + 1][cur_y] = 0
if cur_y - 1 >= 0 and grid[cur_x][cur_y - 1] == 1:
queue.append([cur_x, cur_y - 1])
grid[cur_x][cur_y - 1] = 0
if cur_y + 1 < len(grid[0]) and grid[cur_x][cur_y + 1] == 1:
queue.append([cur_x, cur_y + 1])
grid[cur_x][cur_y + 1] = 0
return
def SumAreaIsolatedLand(self, grid):
m, n = len(grid), len(grid[0])
sumN = 0
for j in [0, -1]:
for i in range(m):
if grid[i][j] == 1:
self.bfs(grid, i, j)
for i in [0, -1]:
for j in range(1, n - 1):
if grid[i][j] == 1:
self.bfs(grid, i, j)
for i, j in product(range(1, m - 1), range(1, n - 1)):
if grid[i][j] == 1:
sumN += 1
return sumN
沉没孤岛
题目描述:
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要将所有孤岛“沉没”,即将孤岛中的所有陆地单元格(1)转变为水域单元格(0)。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。
之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出将孤岛“沉没”之后的岛屿矩阵。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1
提示信息

方案:
与孤岛总面不同的是,需要在原有grid上进行操作,不可以直接对grid进行调整,增加visible来控制非孤岛的位置,最后遍历,仍然为1的便是孤岛
- 深度优先遍历
class Solution:
def dfs(self, grid, visible, i, j):
if (
i < 0
or j < 0
or i >= len(grid)
or j >= len(grid[0])
or grid[i][j] == 0
or visible[i][j] is True
):
return
visible[i][j] = True
self.dfs(grid, visible, i - 1, j)
self.dfs(grid, visible, i + 1, j)
self.dfs(grid, visible, i, j - 1)
self.dfs(grid, visible, i, j + 1)
return
def DownIsolatedLand(self, grid):
m, n = len(grid), len(grid[0])
visible = [[False] * n for _ in range(m)]
for i in [0, -1]:
for j in range(1, n - 1):
if grid[i][j] == 1:
self.dfs(grid, visible, i, j)
for j in [0, -1]:
for i in range(1, m - 1):
if grid[i][j] == 1:
self.dfs(grid, visible, i, j)
for i, j in product(range(1, m - 1), range(1, n - 1)):
if grid[i][j] == 1 and visible[i][j] is False:
grid[i][j] = 0
return
- 广度优先遍历
class Solution:
def bfs(self, grid, visible, i, j):
queue = deque([[i, j]])
visible[i][j] = True
while queue:
cur_x, cur_y = queue.pop()
if (
cur_x - 1 >= 0
and grid[cur_x - 1][cur_y] == 1
and visible[cur_x - 1][cur_y] is False
):
queue.append([cur_x - 1, cur_y])
visible[cur_x - 1][cur_y] = True
if (
cur_x + 1 < len(grid)
and grid[cur_x + 1][cur_y] == 1
and visible[cur_x + 1][cur_y] is False
):
queue.append([cur_x + 1, cur_y])
visible[cur_x + 1][cur_y] = True
if (
cur_y - 1 >= 0
and grid[cur_x][cur_y - 1] == 1
and visible[cur_x][cur_y - 1] is False
):
queue.append([cur_x, cur_y - 1])
visible[cur_x][cur_y - 1] = True
if (
cur_y + 1 < len(grid[0])
and grid[cur_x][cur_y + 1] == 1
and visible[cur_x][cur_y + 1] is False
):
queue.append([cur_x, cur_y + 1])
visible[cur_x][cur_y + 1] = True
return
def DownIsolatedLand(self, grid):
m, n = len(grid), len(grid[0])
visible = [[False] * n for _ in range(m)]
for i in [0, -1]:
for j in range(1, n - 1):
if grid[i][j] == 1:
self.bfs(grid, visible, i, j)
for j in [0, -1]:
for i in range(1, m - 1):
if grid[i][j] == 1:
self.bfs(grid, visible, i, j)
for i, j in product(range(1, m - 1), range(1, n - 1)):
if grid[i][j] == 1 and visible[i][j] is False:
grid[i][j] = 0
return
水流问题
题目描述:
现有一个 N × M 的矩阵,每个单元格包含一个数值,这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界,而矩阵的右边界和下边界被视为第二组边界。
矩阵模拟了一个地形,当雨水落在上面时,水会根据地形的倾斜向低处流动,但只能从较高或等高的地点流向较低或等高并且相邻(上下左右方向)的地点。我们的目标是确定那些单元格,从这些单元格出发的水可以达到第一组边界和第二组边界。
输入描述:
第一行包含两个整数 N 和 M,分别表示矩阵的行数和列数。
后续 N 行,每行包含 M 个整数,表示矩阵中的每个单元格的高度。
输出描述:
输出共有多行,每行输出两个整数,用一个空格隔开,表示可达第一组边界和第二组边界的单元格的坐标,输出顺序任意。
输入示例:
5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1
输出示例:
0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1
提示信息:

图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
解题思路:
从上左边界和右下边界作为始点,水流开始往高处流动,最终取两个方向的交集,说明即可往第一组边界流动,也可以往第二组边界流动
- 深度优先遍历
class Solution:
def dfs(self, grid, nums, i, j):
if i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]) or (i, j) in nums:
return
nums.add((i, j))
if i - 1 >= 0 and grid[i][j] <= grid[i - 1][j]:
self.dfs(grid, nums, i - 1, j)
if i + 1 < len(grid) and grid[i][j] <= grid[i + 1][j]:
self.dfs(grid, nums, i + 1, j)
if j - 1 >= 0 and grid[i][j] <= grid[i][j - 1]:
self.dfs(grid, nums, i, j - 1)
if j + 1 < len(grid[0]) and grid[i][j] <= grid[i][j + 1]:
self.dfs(grid, nums, i, j + 1)
return
def WaterFlow(self, grid):
m, n = len(grid), len(grid[0])
num1 = set()
num2 = set()
for i in range(m):
self.dfs(grid, num1, i, 0)
self.dfs(grid, num2, i, n - 1)
for j in range(n):
self.dfs(grid, num1, 0, j)
self.dfs(grid, num2, m - 1, j)
return list(num1 & num2)
- 广度优先遍历
class Solution:
def bfs(self, grid, nums, i, j):
queue = deque([[i, j]])
nums.add((i, j))
while queue:
cur_x, cur_y = queue.pop()
if (
cur_x - 1 >= 0
and grid[cur_x - 1][cur_y] >= grid[cur_x][cur_y]
and (cur_x - 1, cur_y) not in nums
):
queue.append([cur_x - 1, cur_y])
nums.add((cur_x - 1, cur_y))
if (
cur_x + 1 < len(grid)
and grid[cur_x + 1][cur_y] >= grid[cur_x][cur_y]
and (cur_x + 1, cur_y) not in nums
):
queue.append([cur_x + 1, cur_y])
nums.add((cur_x + 1, cur_y))
if (
cur_y - 1 >= 0
and grid[cur_x][cur_y - 1] >= grid[cur_x][cur_y]
and (cur_x, cur_y - 1) not in nums
):
queue.append([cur_x, cur_y - 1])
nums.add((cur_x, cur_y - 1))
if (
cur_y + 1 < len(grid[0])
and grid[cur_x][cur_y + 1] >= grid[cur_x][cur_y]
and (cur_x, cur_y + 1) not in nums
):
queue.append([cur_x, cur_y + 1])
nums.add((cur_x, cur_y + 1))
return
def WaterFlow(self, grid):
m, n = len(grid), len(grid[0])
num1 = set()
num2 = set()
for i in range(m):
self.bfs(grid, num1, i, 0)
self.bfs(grid, num2, i, n - 1)
for j in range(n):
self.bfs(grid, num1, 0, j)
self.bfs(grid, num2, m - 1, j)
return list(num1 & num2)
建造最大岛屿
题目描述:
给定一个由 1(陆地)和 0(水)组成的矩阵,你最多可以将矩阵中的一格水变为一块陆地,在执行了此操作之后,矩阵中最大的岛屿面积是多少。
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
输入描述:
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述:
输出一个整数,表示最大的岛屿面积。如果矩阵中不存在岛屿,则输出 0。
输入示例:
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
6
提示信息

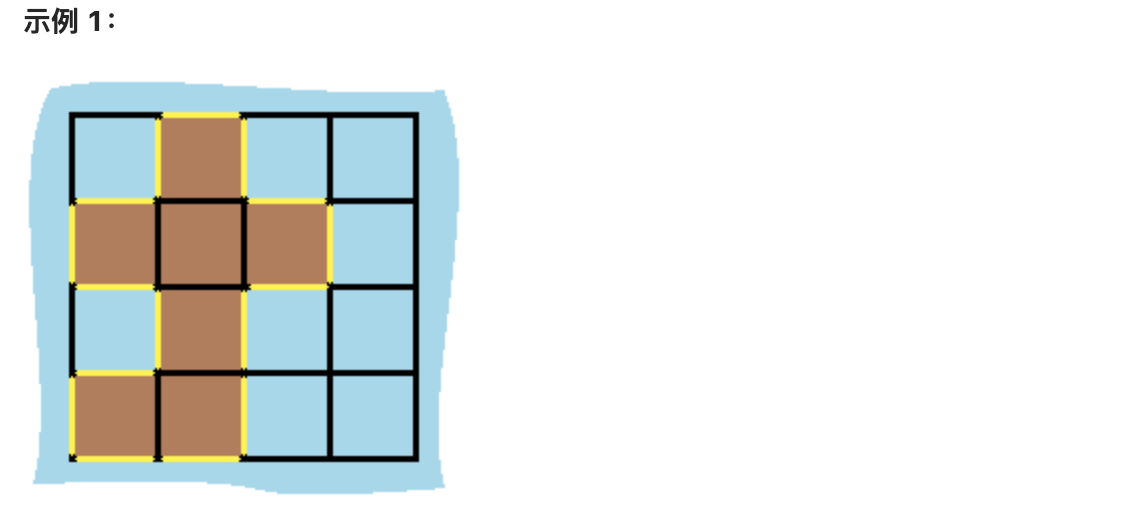
对于上面的案例,有两个位置可将 0 变成 1,使得岛屿的面积最大,即 6。

解决方案:
- 分区遍历,将一块岛屿按照新的序号保留下来,同时计算出对应的面积
- 遍历grid==0的区域,进行连通,确定最大值
- 深度优先遍历:
class Solution:
def dfs(self, grid, index, i, j):
if (
i < 0
or j < 0
or i >= len(grid)
or j >= len(grid[0])
or grid[i][j] in [0, index]
):
return
self.cnt += 1
grid[i][j] = index
self.dfs(grid, index, i - 1, j)
self.dfs(grid, index, i + 1, j)
self.dfs(grid, index, i, j - 1)
self.dfs(grid, index, i, j + 1)
return
def BuildLand(self, grid):
record = {0: 0}
m, n = len(grid), len(grid[0])
index = 2
maxN = 0
for i, j in product(range(m), range(n)):
if grid[i][j] == 1:
self.cnt = 0
self.dfs(grid, index, i, j)
record[index] = self.cnt
index += 1
maxN = max(maxN, self.cnt)
for i, j in product(range(m), range(n)):
if grid[i][j] == 0:
sumN = 1
if i - 1 >= 0:
sumN += record[grid[i - 1][j]]
if i + 1 < m:
sumN += record[grid[i + 1][j]]
if j - 1 >= 0:
sumN += record[grid[i][j - 1]]
if j + 1 < n:
sumN += record[grid[i][j + 1]]
maxN = max(maxN, sumN)
return maxN
- 广度优先遍历
class Solution:
def bfs(self, grid, index, i, j):
queue = deque([[i, j]])
grid[i][j] = index
cnt = 1
while queue:
cur_x, cur_y = queue.pop()
if cur_x - 1 >= 0 and grid[cur_x - 1][cur_y] == 1:
queue.append([cur_x - 1, cur_y])
grid[cur_x - 1][cur_y] = index
cnt += 1
if cur_x + 1 < len(grid) and grid[cur_x + 1][cur_y] == 1:
queue.append([cur_x + 1, cur_y])
grid[cur_x + 1][cur_y] = index
cnt += 1
if cur_y - 1 >= 0 and grid[cur_x][cur_y - 1] == 1:
queue.append([cur_x, cur_y - 1])
grid[cur_x][cur_y - 1] = index
cnt += 1
if cur_y + 1 < len(grid[0]) and grid[cur_x][cur_y + 1] == 1:
queue.append([cur_x, cur_y + 1])
grid[cur_x][cur_y + 1] = index
cnt += 1
return cnt
def BuildLand(self, grid):
record = {0: 0}
m, n = len(grid), len(grid[0])
index = 2
maxN = 0
for i, j in product(range(m), range(n)):
if grid[i][j] == 1:
cnt = self.bfs(grid, index, i, j)
record[index] = cnt
index += 1
maxN = max(maxN, cnt)
for i, j in product(range(m), range(n)):
if grid[i][j] == 0:
sumN = 1
if i - 1 >= 0:
sumN += record[grid[i - 1][j]]
if i + 1 < m:
sumN += record[grid[i + 1][j]]
if j - 1 >= 0:
sumN += record[grid[i][j - 1]]
if j + 1 < n:
sumN += record[grid[i][j + 1]]
maxN = max(maxN, sumN)
return maxN
岛屿的周长
题目描述
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的周长。
输入示例
5 5
0 0 0 0 0
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0
输出示例
14
提示信息

岛屿的周长为 14。
解决方案:
从左上往右下遍历,如果当前位置为1,那周长会增加4,如果当前位置左/下位置也为1,那将会减少2条边,所以只需要计数即可
from itertools import product
class Solution:
def LaneLength(self, grid):
m, n = len(grid), len(grid[0])
cnt1 = 0
cnt2 = 0
for i, j in product(range(m), range(n)):
if grid[i][j] == 1:
cnt1 += 1
if i + 1 < m and grid[i + 1][j] == 1:
cnt2 += 1
if j + 1 < n and grid[i][j + 1] == 1:
cnt2 += 1
return 4 * cnt1 - 2 * cnt2