目录
Floyd算法简单理解:不断加中转点更新最短路,实现多对多最短路径
Floyd算法

又称为Floyd-Warshall算法,是一种用于求解带权有向图中任意两顶点间的最短路径的算法。该算法利用动态规划的思想,通过不断更新顶点对之间的最短路径来实现。Floyd算法的时间复杂度为O(n3),空间复杂度为O(n2),其中n是图中顶点的数量。
简单理解
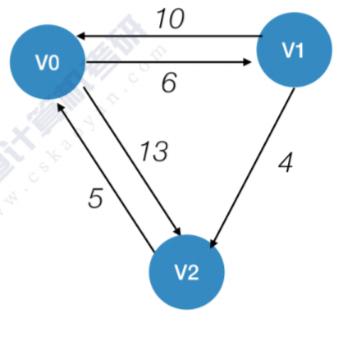
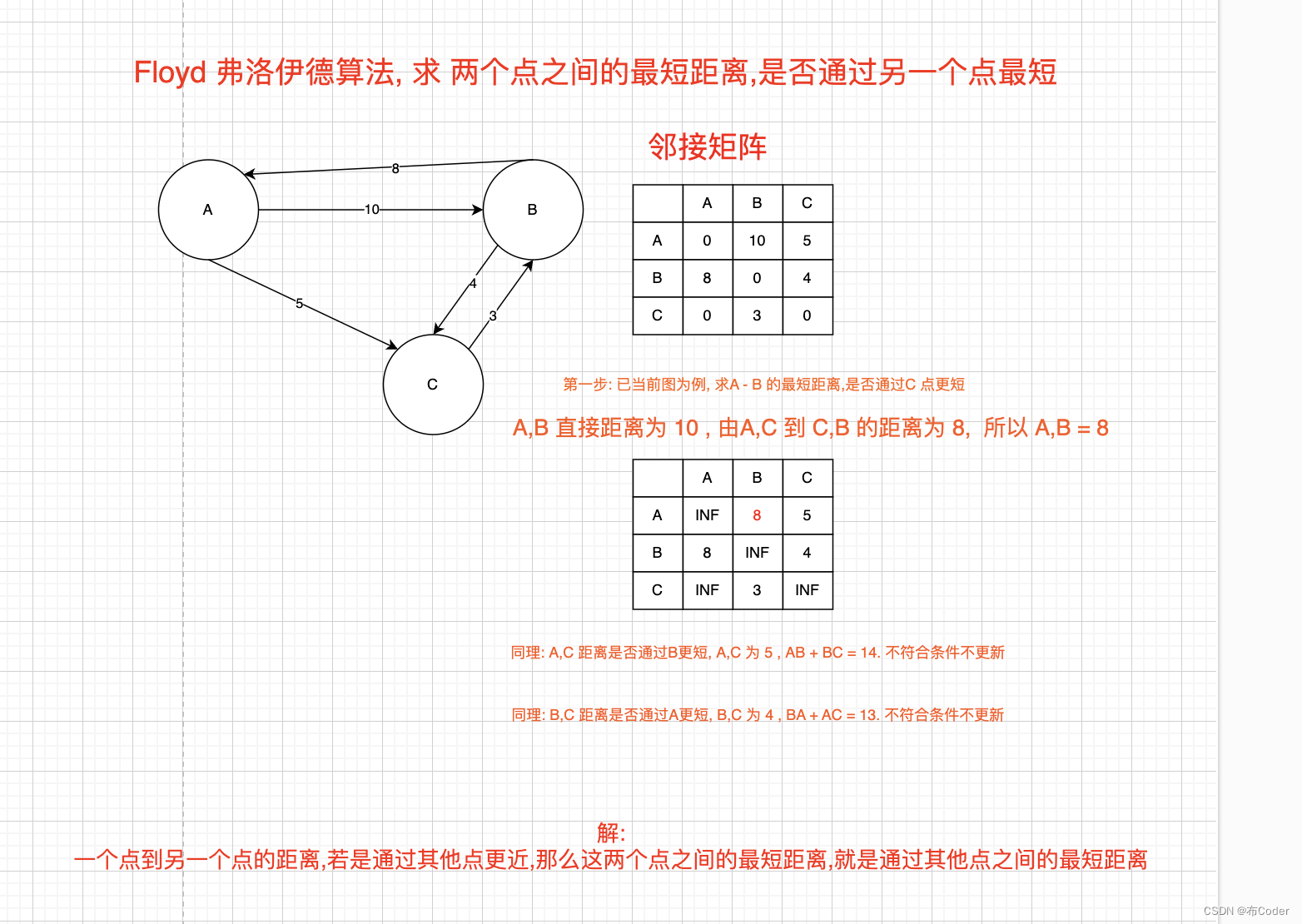
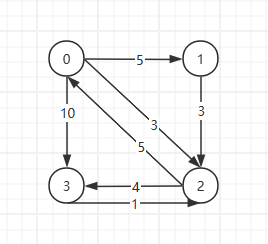
Floyd算法的基本思想是通过考虑图中所有顶点作为潜在的中转点,来逐步更新任意两个顶点之间的最短路径。算法开始时,首先根据图的直接连接关系初始化一个距离矩阵,表示各顶点对之间的直接距离(如果两个顶点之间没有直接连接,则距离设为无穷大)。然后,算法通过三层嵌套循环遍历所有可能的顶点对(i, j)和潜在的中转点k,如果通过中转点k可以使顶点i到顶点j的距离更短,则更新距离矩阵中i到j的距离值。最终,距离矩阵中存储的就是任意两个顶点之间的最短路径长度。