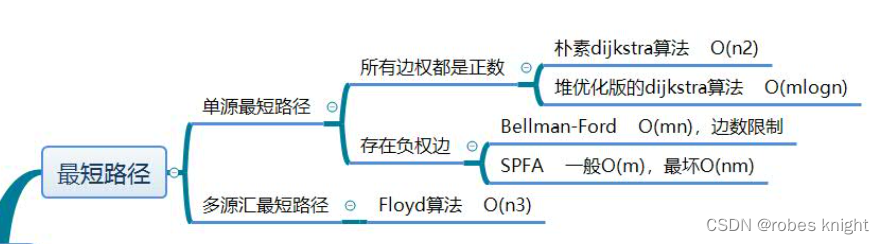
开始编程前分析设计思路和程序的整体的框架,以及作为数学问题的性质:
设计思路:
- 利用邻接表存储图的结构,存储对应顶点和边
- 作为无向图存边时正反都进行存储便于寻找路径
- 对顶点的访问和路径走向进行记录
- 使用回溯法+深度优先对回路进行探索
- 对每一条边进行编号,根据路径走向输出结果
程序流程图:
数学性质:
- 图中的每个顶点恰好被访问一次,并且最后回到起始顶点,形成一个闭合的环
- 另一种表达是一条通过图中所有顶点且仅通过一次的回路,不需要所有边都必须被使用
时间复杂度O(n!)
在寻找哈密顿回路的过程中,使用深度优先搜索的方法。会遍历所有可能的路径,直到找到一个哈密顿回路或者遍历完所有的路径。在完全图中,可能的路径数量是n的阶乘(n!),因为每个顶点都可以是路径的起点。
源代码:
#include <iostream> #include <vector> #include <utility> #include <unordered_map>//使用哈希表 using namespace std; //定义需要的数组及变量 const int MAXN = 100;//最大顶点数 vector<pair<int, int>> graph[MAXN];//邻接表表示图,存储顶点对和边的编号 bool visited[MAXN];//记录顶点是否被访问 int path[MAXN];//存储回路路径 int edgeIndex[MAXN * MAXN];//存储每条边的编号 int n, m;//顶点数和边数 int pathLen;//路径长度 int edgeCount;//边的计数,用于生成编号 //为每条边生成一个唯一的编号 int EdgeIndex(int u,int v){ for (const auto& edge : graph[u]){ if (edge.first == v){ return edge.second; } } return -1;//边不存在的情况 } //使用深度优先寻找回路 bool DFS(int curr, int prev){ visited[curr] = true;//标记当前顶点为已访问 path[pathLen++] = curr;//将当前顶点加入路径 //如果已经访问了所有顶点,即找到了回路 if (pathLen == n){ return true; } //尝试从当前顶点出发访问其他未访问的顶点 for (const auto& edge : graph[curr]){ int next = edge.first; int edgeId = edge.second; if (!visited[next] && (next != prev || pathLen == 1)){ //避免陷入循环,除第一个顶点 if (DFS(next, curr)) { return true; } } } visited[curr] = false;//回溯上一步撤销选择 pathLen--;//路径回退 return false; } //判断是否存在回路 bool Ham(){ fill(visited, visited + n, false);//初始化访问标记和路径长度 pathLen = 0;//初始路径长度 //从每个顶点开始尝试寻找哈密顿回路 for (int start = 0; start < n; ++start) { if (DFS(start, -1)) { return true; } } return false; } //按要求输出路径 void Path(){ cout << "YES" << endl;//按照题目要求先输出YES for (int i = 0; i < n; ++i) { int u = path[i];//找到当前顶点与前一个顶点之间的边的编号 int v = path[(i + 1) % n]; int edgeId = EdgeIndex(u, v); if (edgeId == -1) { cout << "Error" << endl; exit(1);//如果边不存在,则输出错误信息并退出程序 } edgeId++; cout << (u < v ? "": "-") << edgeId << " ";//输出边的编号和方向 } cout << endl; } int main(){ cin >> n >> m;//输入顶点数和边数 for (int i = 0; i < m; ++i) { int u, v; cin >> u >> v;//输入边的两个顶点 u--; v--;//转换为从0开始的索引 //添加边到邻接表,并存储边的编号 graph[u].push_back({v, edgeCount}); graph[v].push_back({u, edgeCount});//作为无向图,两边都添加 edgeCount++;//增加边的计数 } //根据寻找结果进行输出 if (Ham()) { Path();//输出回路路径 } else { cout << "NO" << endl;//若无回路则输出NO } system("pause"); return 0; }
测试用例:(n不小于15,m不小于30;n为顶点数、m为边数)
测试数据1: 测试数据2:
16 32 16 31
1 2 1 2
1 3 8 9
1 16 1 3
2 16 2 2
8 9 9 10
2 3 2 3
2 4 3 4
3 4 3 5
3 5 4 5
4 5 4 6
4 6 9 11
5 6 10 11
5 7 10 12
6 7 8 10
6 8 11 12
7 8 11 13
7 9 5 6
8 10 6 7
9 10 5 7
9 11 12 13
10 12 12 14
10 11 13 14
11 12 6 8
11 13 7 8
12 13 7 9
12 14 1 16
13 14 1 15
13 15 2 16
14 16 15 16
14 15 14 15
15 16 13 15
1 15
输出结果:
数据测试结果1:
YES1 4 -29 -26 -21 -18 -15 -11 -8 9 13 17 20 24 28 -32
数据测试结果2:
YES
1 6 7 9 17 18 24 2 5 12 15 20 22 30 29 -26