目录
一、概述
在点云配准中,四元数法是一种精确计算旋转和平移变换的方法。其目标是找到一个刚体变换,使源点云和目标点云的对应点集之间的误差最小化。四元数法通过利用四元数的性质来优化旋转矩阵的计算,避免了传统方法中的奇异性问题。
1.1 基本思想
1.2详细步骤


二、代码实现
import open3d as o3d
import numpy as np
def solve_transform_quaternion(s, t):
P = np.asarray(s.points)
Q = np.asarray(t.points)
# 判断两个点集中点的个数是否一致
if P.shape[0] != Q.shape[0]:
raise Exception("两个点集不匹配")
else:
n = P.shape[0]
# 1、分别求质心
meanP = np.mean(P, axis=0)
meanQ = np.mean(Q, axis=0)
# 2、去质心
P_ = P - meanP
Q_ = Q - meanQ
# 3、构建协方差矩阵D
D = np.dot(P_.T, Q_)/n
# 4、计算4 X 4 矩阵中所需元素
Dt = np.transpose(D) # D的转置
tr_D = np.trace(D) # D的迹
A_ij = D - Dt
v_A = np.array([[A_ij[1][2], A_ij[2][0], A_ij[0][1]]])
M = D + Dt - tr_D * np.eye(3)
# 5、构建 4 X 4 矩阵
Ql = np.vstack((np.array([[tr_D]]), np.transpose(v_A)))
Qr = np.vstack((v_A, M))
Q = np.hstack((Ql, Qr))
# 6、求 4 X4 矩阵的特征值与特征向量
[eig_v, eig_u] = np.linalg.eig(Q)
i = np.argmax(eig_v) # 最大特征值的位置
q = eig_u[:, i] # 最大特征值对应的特征向量
# 7、由四元数求旋转矩阵
R = o3d.geometry.get_rotation_matrix_from_quaternion(q)
t = meanQ - np.dot(R, meanP) # 计算平移向量
# 8、构建欧式变换矩阵
T = np.eye(4)
T[:3, :3] = R
T[:3, 3] = t
T[3, 3] = 1.0
return T
# ---------------加载点云数据--------------------
source = o3d.io.read_point_cloud("Horse.pcd")
target = o3d.io.read_point_cloud("Horse_trans.pcd")
# ------对初始位置的点云进行颜色渲染--------------
source.paint_uniform_color([0, 1, 0]) # 绿色
target.paint_uniform_color([0, 0, 1]) # 蓝色
o3d.visualization.draw_geometries([source, target], width=800, height=800)
Tran = solve_transform_quaternion(source, target)
print('变换矩阵为:\n', Tran)
align = source.transform(Tran)
align.paint_uniform_color([1, 0, 0]) # 红色
o3d.visualization.draw_geometries([align, target], width=800, height=800)
三、实现效果
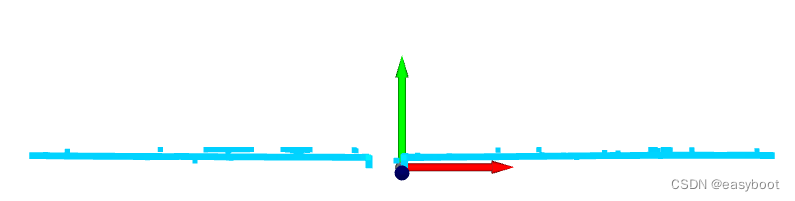
3.1原始点云

3.2配准后点云

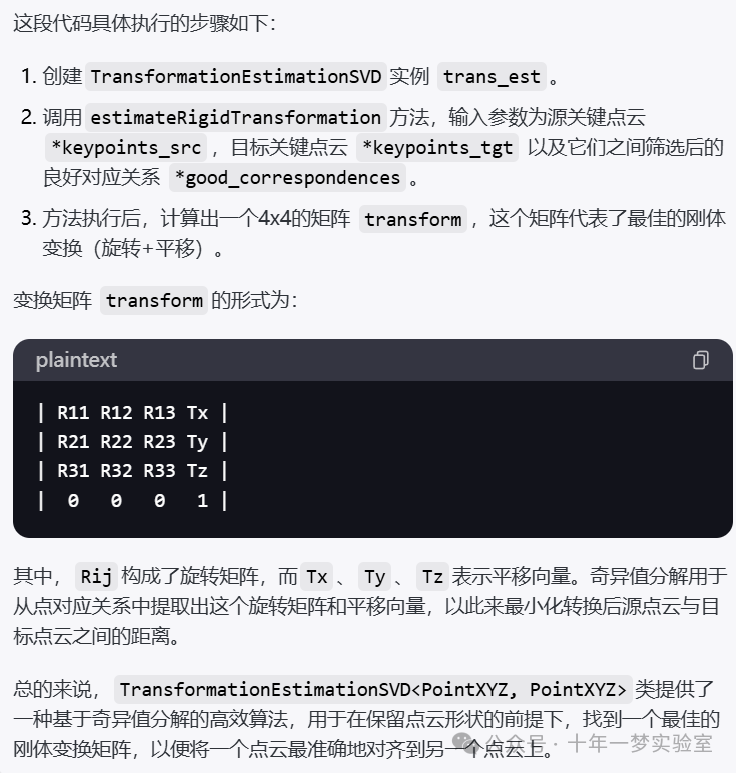
3.3变换矩阵
[[ 1.00000000e+00 1.90151073e-09 1.03664745e-09 1.00000000e-01]
[-6.11550683e-10 7.07106781e-01 -7.07106781e-01 5.00000000e-02]
[-2.07759157e-09 7.07106781e-01 7.07106781e-01 1.00000000e-02]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]