【C++】哈希之位图

一、位图概念

假如有40亿个无重复且没有排序的无符号整数，给一个无符号整数，如何判断这个整数是否在这40亿个数中？

我们用以前的思路有这些：

1. 把这40亿个数遍历一遍，直到找到为为止
2. 排序+二分查找
3. 位图解决

遍历一遍的时间复杂度为O(N)；排序是O(N * logN)，二分查找是O(logN)，第二种还不如第一种。前面两种方法如果是针对比较小的数据的话，还行。但是如果是数据很大的，效率就低了。所以我们可以使用第三种方法，位图解决查找数据的问题。

位图概念：
位图是通过每一个比特位来判断一个数是否是在还是不在。一个二进制比特位只有两种状态，要么为0，要么为1，如果某个数据在，则对应映射的比特位为1；不在，对应的比特位为0。位图适用于海量数据处理，且数据无重复的场景，时间复杂度为O(1)

用位图解决前面的问题：

有40亿个无重复且没有排序的无符号整数，给一个无符号整数，如何判断这个整数是否在这40亿个数中？

首先要了解1G大约等于10亿个字节，1个整数等于4个字节，1个字节等于8个比特位。换算下40亿个整数大约是16G。但是我们不可能开出16G的内存去查找一个数，用位图就可以节省很多空间了。一个整数等于32个比特位，根据位图的概念，用每个比特位是1还是0来确定一个数到底在不在，1个整数的32个比特位可以用来确定32个数据的存在，所以16G除以32等于0.5G，即512M，这就是开辟的空间大小，是不是节省多了。

这里是我们自己模拟出来的一个简单的位图，主要有以下接口：

1️⃣构造
使用vector的接口resize开辟出N / 32 + 1的空间大小，每个位置初始化为0，为什么要除32？因为一个整数有32个比特位，这32个比特位存储在vector数组的一个位置里；为什么又要加1？因为假如开的空间大小是50，50/32等于1，那到底是一个位置还是2个位置？很明显是2个，第一个位置刚好满32个比特位，剩余18个比特位也要有位置放，因此要有第二个位置。

2️⃣将该比特位设置为1
每个数都有对应映射的比特位，将这个数除以32找到该数在数组中的位置，取模32找到映射的第几个比特位，1左移前面取模的位数，然后按位或将该比特位设置为1

3️⃣将该比特位设置为0
前面同上，先按位取反1左移前面取模的位数后的数，然后按位与将该比特位设置为0

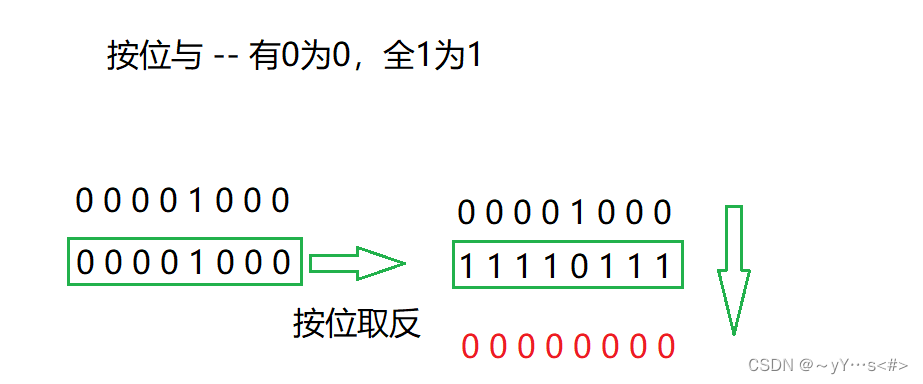
4️⃣判断状态
前面同上，用按位与，映射的位置和1移动后的位都是1才说明这个数在

类的模板是非类型模板参数，传的是数据的大小。成员变量是vector类型，方便开辟空间。为什么1是左移？注意：左移不是真的往左边移，右移也不是真的往右边移，跟方向没关系。左移是往高位移动，右移是往低位移动；其次，还要看编译器，vs下是小端存储数据的，所以这里是左移。

代码：

namespace yss
{
	template<size_t N>
	class bitset
	{
	public:
		//构造
		bitset()
		{
			_bit.resize(N / 32 + 1, 0);
		}
		//该比特位 置为1
		void set(size_t x)
		{
			size_t i = x / 32;
			size_t j = x % 32;
			_bit[i] |= (1 << j);
		}
		//该比特位 置为0
		void reset(size_t x)
		{
			size_t i = x / 32;
			size_t j = x % 32;
			_bit[i] &= ~(1 << j);
		}
		//该比特位的状态（在/不在）
		bool test(size_t x)
		{
			size_t i = x / 32;
			size_t j = x % 32;
			return _bit[i] & (1 << j);
		}

	private:
		vector<int> _bit;
	};
}

void Func1()
{
	yss::bitset<100> bs;
	bs.set(30);
	bs.set(60);
	bs.set(90);
	for (size_t i = 0; i < 100; i++)
	{
		if (bs.test(i))
		{
			cout << i << "->" << "在" << endl;
		}
		else
		{
			cout << i << "->" << "不在" << endl;
		}
	}
}

40亿个数据，如下：

yss::bitset<-1>* bs = new bitset<-1>;//第一种写法
yss::bitset<4294967295>* bs = new bitset<4294967295>;//第二种写法

栈的空间有限，对于很大的数据，需要大量的内存空间，应该通过堆来申请。其他同上面代码。

二、海量数据面试题

1️⃣给定100亿个整数，设计算法找到只出现一次的整数？

思路：

• 使用两个位图来实现，表示00(没有出现) - 01(出现一次) - 10 - 11 的情况（后面两个是出现2个及2个以上），本题是找到只出现一次的整数，所以最终判断这个整数在不在的条件是两个位图映射的比特位是不是01
• 有100亿个整数，为了映射所有整数，一个位图开辟的空间大小是512M，即2的32次方个比特位，两个合起来是占1G内存

代码：

int main()
{
	vector<int> a{ 2,2,3,3,5,8,8,14,14,66 };
	bitset<-1>* bs1 = new bitset<-1>;//指针
	bitset<-1>* bs2 = new bitset<-1>;
	
	for (auto e : a)
	{
		if (bs1->test(e) == false && bs2->test(e) == false)
		{
			bs2->set(e);//00->01
		}
		else if (bs1->test(e) == false && bs2->test(e) == true)
		{
			bs1->set(e);
			bs2->reset(e);//01->10
		}
		else
		{
			//
		}
	}
	for (size_t i = 0; i < -1; i++)
	{
		if (bs1->test(i) == false && bs2->test(i) == true)
		{
			cout << i << endl;// 5   66
		}
	}
	return 0;
}

2️⃣给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

思路：

• 既然给两个文件，那么也要用两个位图。100亿个整数，跟前面一样，一个位图也是512M，两个位图刚好1G
• 只需判断某个数据在两个位图是否存在即可，如果两个位图的对应映射的比特位都是1，就是交集；反之，有一个不是1，或者两个都是0就不是交集

代码：

int main()
{
	vector<int> a1{ 2,4,6,8,10,14,20 };
	vector<int> a2{ 1,3,4,5,7,9,10,17 };
	bitset<-1>* bs1 = new bitset<-1>;
	bitset<-1>* bs2 = new bitset<-1>;
	for (auto e : a1)
	{
		bs1->set(e);
	}
	for (auto e : a2)
	{
		bs2->set(e);
	}
	for (size_t i = 0; i < -1; i++)
	{
		if (bs1->test(i) == true && bs2->test(i) == true)
		{
			cout << i << endl;// 4  10
		}
	}
	return 0;
}

3️⃣1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

思路：

• 步骤同问题1，在它的基础上增加了10->11的情况，即出现3次和3次以上，然后最后判断条件为出现1次和2次的数据打印出来

代码：

int main()
{
	vector<int> a{ 2,4,4,5,5,5,7,9,9,9,9 };
	bitset<-1>* bs1 = new bitset<-1>;
	bitset<-1>* bs2 = new bitset<-1>;
	for (auto e : a)
	{
		if (bs1->test(e) == false && bs2->test(e) == false)
		{
			bs2->set(e);//00->01 出现1次
		}
		else if (bs1->test(e) == false && bs2->test(e) == true)
		{
			bs1->set(e);
			bs2->reset(e);//01->10 出现2次
		}
		else if (bs1->test(e) == true && bs2->test(e) == false)
		{
			bs2->set(e);//10->11 出现3次
		}
		//3次以上
	}
	for (size_t i = 0; i < -1; i++)
	{
		if ( (bs1->test(i) == false && bs2->test(i) == true)
			|| (bs1->test(i) == true && bs2->test(i) == false))
		{
			cout << i << endl;// 2  4  7
		}
	}
	return 0;
}