由平行公设的不同而来三种几何学浅谈
欧几里德的《几何原本》
欧几里德的《几何原本》一开始就给出了23个定义,5个公设,5个公理。
23个定义(部分):
点是没有部分的东西。
线是没有宽度的长度。
线的端点是点。
直线是各点都在同一方向上的线。
面是只有长度和宽度的东西。
...
5个公设:
从任何一点到任何一点都可以画一条直线。
有限的直线可以连续地延长成为直线。
以任何一点为圆心,任何距离为半径,可以画一个圆。
所有的直角都相等。
如果一条直线与两条直线相交,在同一平面内同侧的两个内角和小于两个直角,则这两条直线必定相交,而且在这两个角和小于两个直角的那一边相交。(平行公设)
5个公理:
相等的量与相等的量相加,其结果仍然相等。
相等的量与相等的量相减,其结果仍然相等。
重合的量是相等的。
整体大于部分。
两个相等的量的一半也相等。
从现代数学的角度来看,欧几里得的这些定义、公设和公理虽然具有开创性意义,但也存在一些问题:
有些定义缺乏严谨性,如"点是没有部分的东西"并没有给出点的明确定义。现代数学中,点通常被视为原始概念,无需定义。
有些公设和公理并不独立,如第4个公理"整体大于部分"可以从其他公理推导出来.
欧几里得在《几何原本》中提出的"定义"、"公设"、"公理"为几何学的公理化奠定了基础,但其概念与现代数学有所不同。
欧几里得在《几何原本》中提出的"定义"、"公设"、"公理"虽然为后世几何学的发展奠定了基础,但其概念和现代数学有所不同。
欧几里得的"定义"是对点、线、面等基本几何对象的描述,而现代数学的定义更加严谨和抽象。
欧几里得的"公设"是他认为不需要证明的命题,是建立几何学体系的基础。这在一定程度上类似于现代数学的公理。
欧几里得的"公理"则更接近于我们现在所说的"基本性质"或"定理",是他认为可以直接从定义中得到的一些命题。
相比之下,现代数学中的"公理"有更加严格的定义:它是一个形式系统的起始点,是一组我们假定为真的命题,所有定理都由公理通过逻辑推理得到。公理需要满足独立性、相容性和完备性。
现代数学在欧几里得的基础上,发展出了更加严谨、抽象的公理化方法。在现代几何学中,我们通常从一组未定义的概念(如点、线)和一组公理出发,通过逻辑推理来建立整个几何学体系。这种方法使得几何学的基础更加稳固,也让我们能够研究各种不同的几何体系。
尽管存在这些问题,但欧几里得的《几何原本》对数学发展的贡献是巨大的。它首次尝试用公理化的方法来构建数学理论,为后世的公理化运动奠定了基础。同时,它也揭示了公理选取的重要性和复杂性。
平行公设
平行公设是欧几里得在其著作《几何原本》中提出的五条公设之一,也称为欧几里得第五公设。它是关于平行线的性质,在欧几里得几何中起着至关重要的作用。平行公设的原始表述如下:
如果一条直线与两条直线相交,在同一平面内同侧的两个内角和小于两个直角,则这两条直线必定相交,而且在这两个角和小于两个直角的那一边相交。
这个表述比较难以理解,后来数学家们对其进行了改述,有多种等价形式,如:
经过直线外一点,有且仅有一条直线与已知直线平行。
三角形内角和等于180°。
存在相似但不全等的三角形。
四边形的四个内角和等于360°。
从形式上看相差很远,如何理解它们等价?
“经过直线外一点,有且仅有一条直线与已知直线平行”与“三角形内角和等于180°”的等价性:
如果在平面上,经过直线外一点确实有且仅有一条直线与已知直线平行,这意味着平行线之间的性质保证了在任何给定的平面几何系统中,构建的任何三角形的内角和都会是一个固定值。因为当你使用这个平行公设来构造一个三角形时,无论如何延长这个三角形的两边直到它们相交,形成的相交角都将保证内角和为180°,这是因为根据平行线的性质,交替内角相等,从而使得三角形的内角和等于直线上相邻两角的和,即180°。
反之,如果每个三角形的内角和都是180°,这也意味着在通过一点只能画出一条与给定直线平行的线,因为如果存在第二条这样的线,它会与三角形的内角和产生矛盾,因为它将导致可以构造一个内角和不为180°的三角形。因此,这两个命题在逻辑上是等价的。
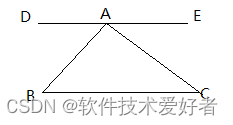
“三角形内角和等于180°”与“存在相似但不全等的三角形”的等价性:
如果三角形内角和等于180°,那么我们可以通过改变三角形的边长但保持其角度不变来构造相似但不全等的三角形。
反之,如果存在相似但不全等的三角形,那么根据相似三角形的定义,它们的对应角相等。设两个三角形分别为ABC和A'B'C',其中∠A等于∠A',∠B等于∠B',∠C等于∠C'。那么∠A+∠B+∠C = ∠A'+∠B'+∠C'。但因为它们是两个不同的三角形,所以上式只能等于180°。
“存在相似但不全等的三角形”与“四边形的四个内角和等于360°”的等价性:
如果存在相似但不全等的三角形,那么我们可以通过将两个这样的三角形拼接成一个四边形,其四个内角的和必然等于两个三角形的内角和,即360°。
反之,如果四边形的四个内角和等于360°,那么我们可以将其对角线连接,将四边形分成四个三角形。根据三角形内角和定理,每个三角形的内角和都等于180°。现在,我们可以改变对角线的长度但保持其方向不变,这样就能得到四个相似但不全等的三角形。
三种几何学
第五个公设非常罗嗦,没有前四个简洁好懂。声明的也不是存在的东西,而是欧几里德自己想的东西。 这就足以说明他的天才。从欧几里德提出这个公理到1800年这大约2100年的时间里虽然人们没有怀疑整个体系的正确性,但是对这个第五公设却一直耿耿于怀。
19世纪,数学家们开始尝试否定平行公设,发现可以建立与欧几里得几何截然不同但同样自洽的非欧几何,如双曲几何和椭圆几何。这表明平行公设是独立于其他公设的,不能被证明。
根据平行公设的不同,几何学可以分为三种:欧几里得几何、罗巴切夫斯基几何和黎曼几何。
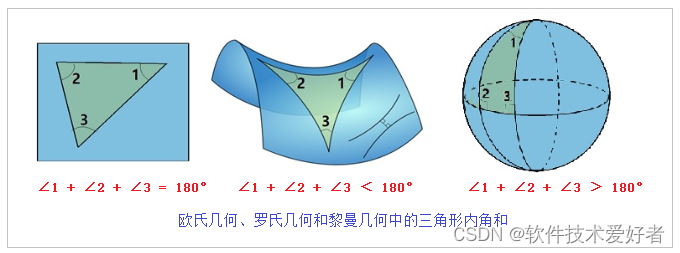
欧几里得几何(Euclidean geometry):
欧几里得几何是最早建立的几何学体系,也是中学阶段学习的主要内容。其平行公设为:经过直线外一点,有且仅有一条直线与已知直线平行。在欧几里得几何中,空间是平直的,两条平行线永远不会相交。三角形内角和等于180°,正方形对角线长度为边长的√2倍等。
罗巴切夫斯基几何(Lobachevskian geometry):
罗巴切夫斯基几何又称双曲几何(hyperbolic geometry),其平行公设为:经过直线外一点,至少有两条直线与已知直线平行。在这种几何学中,空间是负曲率的,平行线有无数条,且会渐渐远离。三角形内角和小于180°,且角和与面积成正比。
黎曼几何(Riemannian geometry):
黎曼几何又称为椭圆几何(elliptic geometry),其平行公设为:经过直线外一点,没有直线与已知直线平行。在黎曼几何中,空间是正曲率的,类似于球面,没有平行线的概念。两条直线必定相交,三角形内角和大于180°。
这三种几何学在数学发展史上具有重要意义。非欧几何的出现打破了欧几里得几何的独尊地位,拓宽了人们对空间的理解。黎曼几何为后来的广义相对论提供了数学基础。不同的几何学在不同领域都有应用,如欧几里得几何用于日常工程,双曲几何用于特殊相对论等。
尽管这三种几何学在性质上差异很大,但它们并不矛盾。因为它们建立在不同的公理系统之上,而数学的一个重要特点就是,在给定公理系统下,所有推导出的定理都是自洽的。正如爱因斯坦所说:"就数学而言,一条定理只要不包含矛盾就是正确的,而与现实世界是否相符无关。"
欧几里得几何、罗巴切夫斯基几何和黎曼几何并不存在本质上的矛盾,它们是建立在不同公理系统上的自洽的数学理论。这三种几何学的不同在于它们对平行线公设的不同处理,导致了它们在性质上的差异。
欧几里得几何:
欧几里得几何是我们最熟悉的几何学,它适用于日常生活中的大部分情况。在欧几里得几何中,空间是平直的,平行线不会相交,三角形内角和等于180°等。这种几何学在建筑、工程、导航等领域有广泛应用。然而,当我们考虑极大尺度(如宇宙)或极小尺度(如原子)时,欧几里得几何就不再适用了。
罗巴切夫斯基几何:
罗巴切夫斯基几何,也称双曲几何,适用于描述负曲率空间。在这种几何中,平行线有无数条,三角形内角和小于180°。爱因斯坦的狭义相对论就是建立在类似罗巴切夫斯基几何的闵可夫斯基空间之上的。此外,双曲几何在某些计算机图形学领域也有应用,如在创建虚拟现实环境时。
黎曼几何:
黎曼几何,也称椭圆几何,适用于描述正曲率空间。在这种几何中,没有平行线,两条直线总会相交,三角形内角和大于180°。黎曼几何在广义相对论中得到了应用,爱因斯坦用它来描述引力场下的时空弯曲。此外,黎曼几何还在微分几何、拓扑学等数学分支中有重要地位。
总的来说,这三种几何学适用于描述不同性质的空间,它们共同构成了我们对空间的几何学理解。在实际应用中,我们需要根据具体问题选择适当的几何学模型。同时,这三种几何学的发现也极大地拓宽了我们的思维空间,让我们认识到数学的真理可以有多种形式。