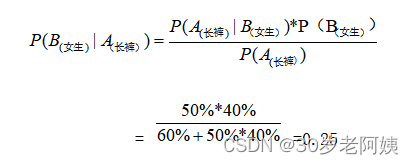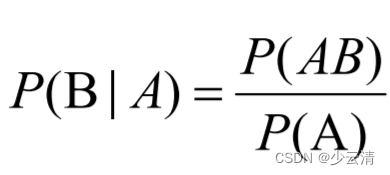目录
1. Bayes Theorem
1.1 先验概率和后验概率
- 先验概率:根据已有的概率分布,推测未发生事件的概率。e.g. 已有天气数据,推测明天是否下雨。
- 后验概率:根据已发生的事件事实 evidence,推测以前数据的概率分布。e.g. 以前的天气数据因为涂鸦损坏丢失了一部分,已知道现在天气下雨,推测以前天气数据的概率分布。
随机事件:是指随机试验中可能发生或不发生的结果。
- 样本空间:是指在一次随机试验中所有可能结果的集合,通常用S或
表示。每一个可能的结果称为样本点。
1.2 条件概率
,表示在B发生的条件下,A发生的概率。
,表示在A发生的条件下,B发生的概率。
1.3 联合概率
,表示事件A和B同时发生的概率。
,“事件A发生概率 * 事件A发生的条件下,B发生的概率”。先写事件A发生概率,然后写乘以条件概率P(B|A),比较好记忆。
,“事件B发生概率 * 事件B发生的条件下,A发生的概率”。先写事件B发生概率,然后写乘以条件概率P(A|B),比较好记忆。
=》贝叶斯定理
1.4 贝叶斯定理
1.4.1 Bayes Formulation - 1
- H,表示先验概率 hypothesis
- E,表示后验事实 evidence
=》P(E)一般是指后验概率,它的概率计算很复杂,因为是已发生事实事件Evidence,需要对所有样本进行测试,才能得到事实概率!
1.4.2 Bayes Formulation - 2
用表示不发生的概率,
,P(E)可以分为两部分,一部分是E和H的交集,另一部分是E和
的交集。
1.5 Bayes 全概率公式
从二概率公式推广到多概率贝叶斯公式。
全概率公式:
贝叶斯全概率公式: