同样是最小生成树,普利姆算法是从一个起始顶点开始,逐步扩展生成树,每次选择连接生成树和未包含顶点的最小边。而克鲁斯卡尔算法是按权值排序的方式,从最小的边开始逐步添加到生成树中,确保不会形成环,直到生成树包含所有顶点。
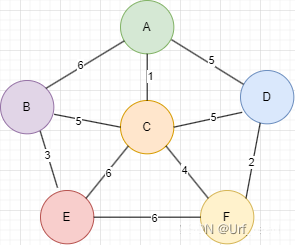
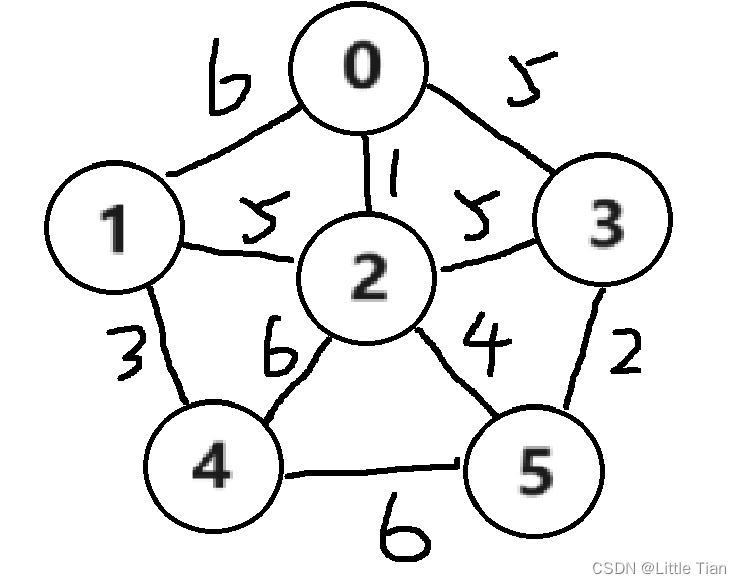
假设我有下面的一个图,克鲁斯卡尔算法就是把这些带权值的边进行排序,然后添加到树中并确保不会成环。
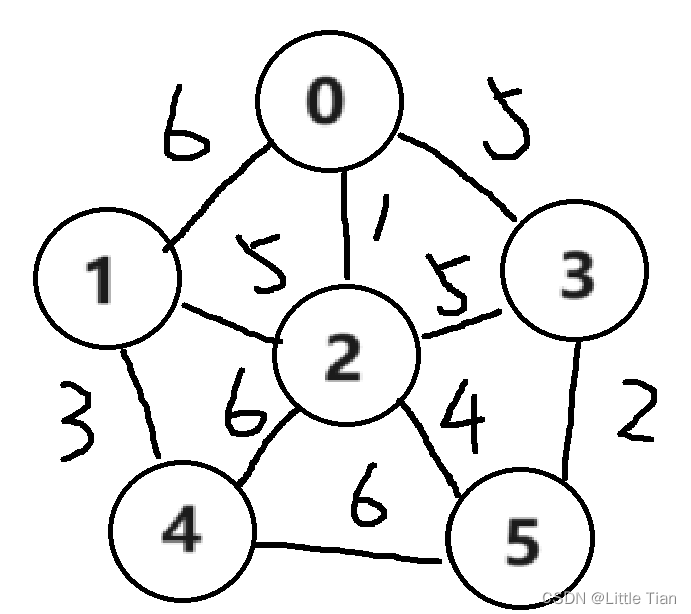
第一步:首先遍历所有边,记录边的前驱和后继(判断是否有环会使用到),并进行排序,这里只列举了全三个边。

第二步:将边添加到树(直接打印前驱后继顶点和权值即可),检查是否有环,这一步该如何实现?
有环的情况如下,假设 0->2 是最先加入到树的边,其次是 2->1 ,最后是 1->0 ,因为 0 是 2 的前驱,2 是 1 的前驱,那么我们可以让 0 是 1 的前驱,这样我们只需要检查 1 的后继是不是等于前驱即可,结果是等于,所以不能纳入。

可以这样理解:0->2 是链表,2->1 增加了链表的长度,但是1,2都属于 0 这个头节点的集合,所以当新链加入时要判断新练的尾节点是否是头节点,如果是,就说明链表有环。
以上可以用结构体来实现。
第三步:遍历第二步,遍历一共 图的边数 次。
接下来是代码部分:
首先是结构体 边(Edge) 的构建:然后创建一个数组用于存放这些边,并且对边进行初始化。
我们可以观察到边的二维数组是关于正对角线对称的,这是因为无向图权值会出现两次,例如:0->1 和1->0 都是 6,所以我们只需要在正对角线的一侧来寻找边即可,如果在整个图中寻找边最后会找到两组相同的边。这也是为什么 for 循环的条件一个是 i 一个是 i+1。

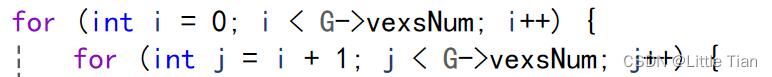
typedef struct Edge {
int start;
int end;
int weight;
}Edge;
Edge* EdgeInit(Graph* G) {
int index = 0;
Edge* E = (Edge*)malloc(sizeof(Edge) * G->arcsNum);
for (int i = 0; i < G->vexsNum; i++) {
for (int j = i + 1; j < G->vexsNum; j++) {
if (G->arcs[i][j] != Max) {
E[index].start = i;
E[index].end = j;
E[index].weight = G->arcs[i][j];
index++;
}
}
}
return E;
}接着是边的排序:这里是简单的冒泡排序,让边数组的顺序根据权值大小从小到大排序。
void Edgesort(Edge* E,Graph* G) {
for (int i = 0; i < G->arcsNum; i++) {
for (int j = i + 1; j < G->arcsNum; j++) {
if (E[j].weight < E[i].weight) {
Edge tmp ;
tmp = E[i];
E[i] = E[j];
E[j] = tmp;
}
}
}
}最后是函数主体:
1.connected数组是存顶点的前驱节点,用来表示该顶点在哪个顶点的集合内(相当于链表的头节点)。第一个for循环初始化该数组,因为初始前驱节点都是本身。
2.第二个for循环是为了遍历每条边,如果边的前驱和后继相等,那么不打印也即是不纳入树。
3.第三个for循环是更新connected数组,更新顶点的前驱节点。
void Kurskal(Edge* E, Graph* G) {
Edgesort(E,G);
int* connected = (int*)malloc(sizeof(int) * G->vexsNum);
for (int i = 0; i < G->vexsNum; i++) {
connected[i] = i;
}
for (int j = 0; j < G->arcsNum; j++) {
int start = connected[E[j].start];
int end = connected[E[j].end];
if (start != end) {
printf(" %c -> %c ,weight = %d", G->vexs[start], G->vexs[end], E[j].weight);
printf("\n");
for (int a = 0; a < G->arcsNum; a++) {
if (connected[a] == end ) {
connected[a] = start;
}
}
}
}
}下面看一个例子用来理解最后一个for循环:
首先最小的是 0->2 边,权值为1。那么就会打印 0->2,然后更新connected数组:由左图变成右图,把connected[2]更新为connected[0],也就是说 2 的前驱是 0 ,那么它就在 0 的集合内(链表内)。


假设说现在又有 2->1 边进入,那么connected数组变化如下:这时的start是0,end是1,把connected[1]的值更新为connected[2],表示纳入该集合(链表)。

现在又有一个边 1->0 进入,现在connected[1]和connected[0]的位置都是0,也就是start等于end,这时还纳入就会造成成环问题,所以不进入if语句,不进入树。
以上就是最后一个for循环的解释。

这就是文章的全部内容了,希望对你有所帮助,如有错误欢迎指出。