目录
8.1 排序相关概念
- 排序码:排序的依据,也称关键码
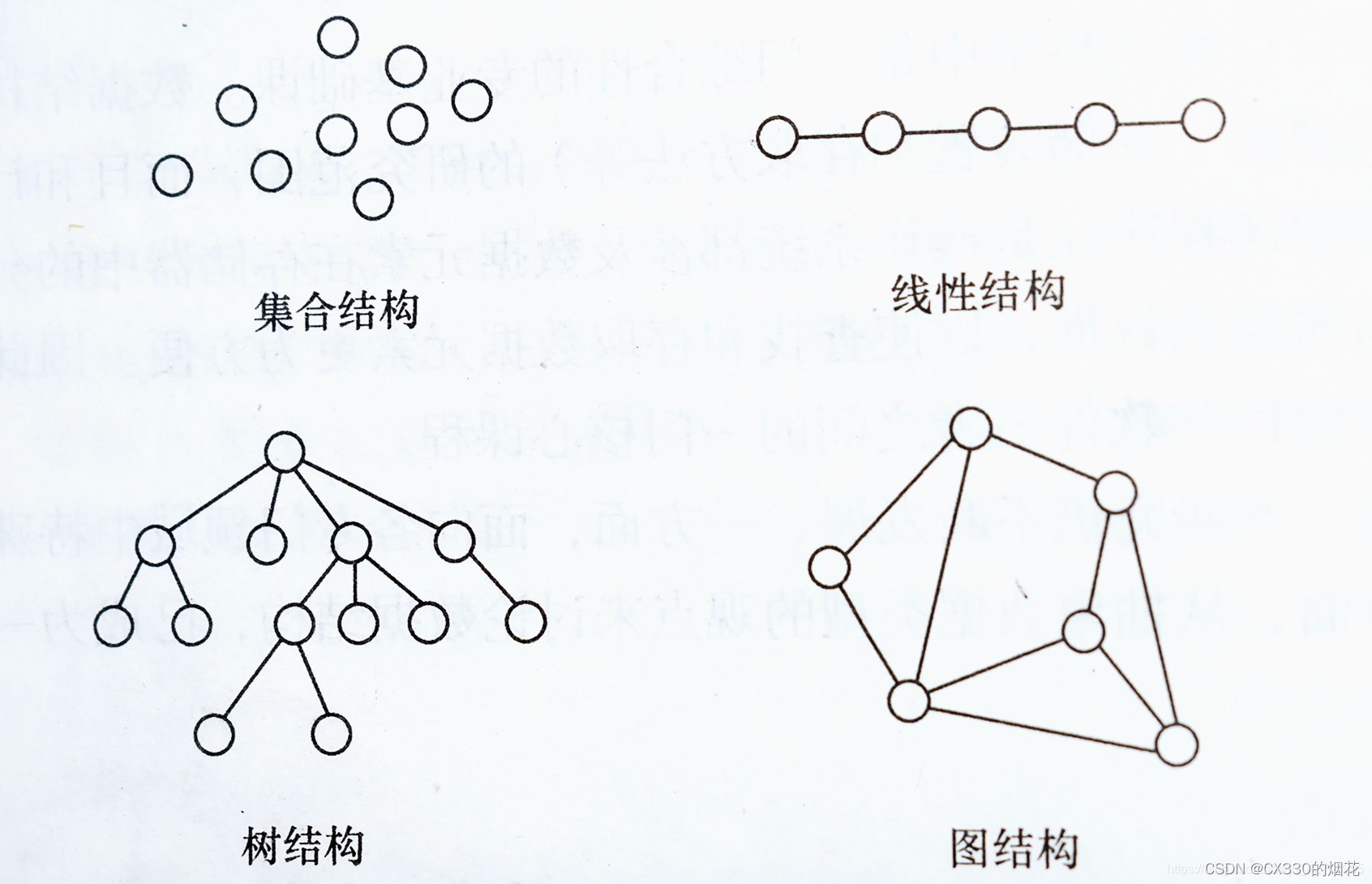
- 排序是对线性结构的一种操作
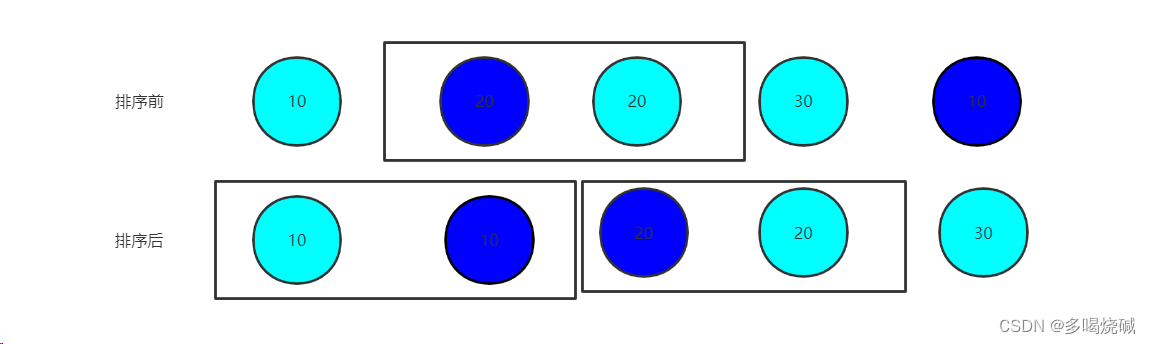
- 排序算法的稳定性:假定在待排序的记录序列中存在多个具有相同关键码的记录,若经过排序,这些记录的相对次序保持不变,则称这种排序算法稳定,否则为不稳定。
- 根据排序过程中所有记录是否全部放在内存中,排序方法分为
(1) 内排序:过程中,待排序的所有记录全部放在内存中
(2) 外排序:过程中,需要在内外存之间交换数据
- 根据排序方法是否建立在关键码比较的基础上,排序方法分为:
(1) 基于比较:通过关键码之间的比较和记录的移动实现。(包括插入排序、交换排序、选择排序和归并排序)
(2) 不基于比较:根据待排序数据的特点所采取的其他方法。(基数排序)
8.2 插入排序
8.2.1 直接插入排序:
基本思路:有将数组分为有序区和无序区,初始时有序区只有一个元素,将无序区的元素一个一个插入有序区,直到所有元素都在有序区内。
# 直接插入排序
def InsertSort(R):
for i in range(1,len(R)):
if R[i]<R[i-1]:
temp = R[i] # 取出无序区的第一个元素
j = i-1 # 前面都是有序的,在有序区中找插入的位置
while True:
R[j+1] = R[j] # 将大于temp的元素后移,空出一个插入的位置
j-=1
if j<0 or R[j]<=temp:
break
R[j+1] = temp
return R
8.2.2 折半插入排序:
折半插入排序和直接插入排序思路差不多,不过在将无序区元素插入有序区时用折半的方法插入。只是优化了插入的部分。
8.2.3 希尔排序:
基本思路:先将整个待排序记录序列分隔成若干个子序列,在子序列内分别进行直接插入排序,待整个序列基本有序后,再对整体记录进行一次直接插入排序。
步骤:
(1) 相邻d个位置的元素分为一组,d=n/2(d是增量)
(2) 将排序序列分为d个组,在各组内进行直接插入排序
(3) 递减d=d/2,重复第二步,直到d=0为止
希尔算法的时间复杂度难以分析,一般认为其平均时间复杂度为O(n1.58)。希尔排序的速度通常要比直接插入排序快。
希尔排序是一种不稳定的排序算法

8.3 交换排序
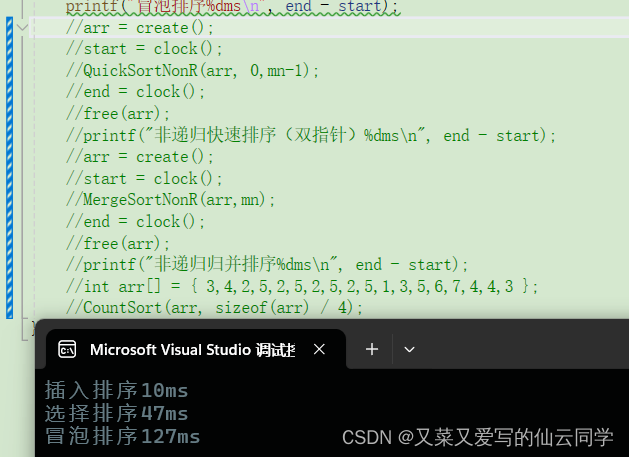
8.3.1 冒泡排序:
基本思路:两个元素反序时进行交换
冒小泡:从后往前看,如果后面的比前面的小就交换。
若某一趟没有出现元素交换,说明所有元素已排好序了。
# 冒泡排序
def BubbleSort(R):
for i in range(len(R)-1):
exchange = False
for j in range(len(R)-1,i,-1):
if R[j]<R[j-1]:
R[j],R[j-1] = R[j-1],R[j]
exchange=True
if exchange == False:
return R8.3.2 快速排序:
先选择一个基准(一般是第一个元素),将待排序记录划分为两部分,左侧关键码小于基准,右侧关键码大于基准,将基准值与左侧最后一个值交换位置,使得基准值在中间。然后分别对左右部分重复上述过程,直到排好。

【例题】

快速排序过程可以用递归树表示

#快速排序
def quickSort(lst,l,r):
if r<=l:
return
q = partition(A,l,r)
quickSort(A,l,q-1)
quickSort(A,q+1,r)
def partition(A,l,r): #将元素进行随机划分
p = randint(A[l],A[r])
A[p],A[r] = A[r],A[p]
i = l
for j in range(l,r-1):
if A[j]<=A[r]:
A[i],A[j] = A[j],A[i]
i+=1
A[i],A[r] = A[r],A[i]
return i8.4 选择排序
8.4.1 简单选择排序
分为无序区和有序区,每趟在无序区中选出最小的记录minj,将minj和有序区后一个数字交换。
是一种不稳定的排序方法
# 简单选择排序
def SelectSort(R):
for i in range(len(R)-1):
minj = i
for j in range(i+1,len(R)):
if R[j]<R[minj]: # 从无序区选最小元素
minj = j
if minj!=i:
R[i],R[minj] = R[minj],R[i]8.4.2 堆排序
堆是完全二叉树
堆的存储是顺序的
堆的定义:大根堆,小根堆
大根堆:父结点的关键字大于子结点的关键字
步骤:
(1)根据序列用广度优先构建一个完全二叉树,上滤(自底向上)调整为大根堆
(2)输出堆顶元素,然后用堆尾元素代替堆顶
(3)从根节点筛选,使其形成一个堆(此时的根节点就是之前的堆尾元素)
筛选:将根节点与左右孩子的较大者进行交换,一直进行到所有子树均为堆或将调整结点交换到叶子位置。
(4)重复二三步骤(n-1次),得到有序序列
【例题】

8.5 归并排序
基础思路:将两个位置相邻的有序子序列归并为一个有序序列
归并要做 趟,每趟归并时间为O(n)


#归并排序,给列表A中下标从l到r的区间排序
def mergeSort(A,l,r):
if r-l<=1:#边界条件处理
return
mid = (l+r)//2
mergeSort(A,l,mid)#递归调用
mergeSort(A,mid,r)
merge(A,l,mid,r)#递推到当前层
def merge(A,l,mid,r): #合并数组A[l,m-1]和A[m,r-1]
l = A[l,mid-1]
r = A[mid,r-1]
k = 0
i = 0
j = 0
while k<=r-l:
if l[i]<=r[j]:
i +=1
A[K] = l[i]
else:
A[K] = r[j]
j+=1
k+=18.6 排序算法复杂度
基于比较排序算法的平均时间复杂度不可能优于



































![AGI 之 【Hugging Face】 的【文本分类】的[数据集][文本转换成词元]的简单整理](https://img-blog.csdnimg.cn/direct/d35548882c924612aadf3dab23f14c7a.jpeg)