2024.2.20力扣每日一题——从前序和中序遍历序列构建二叉树

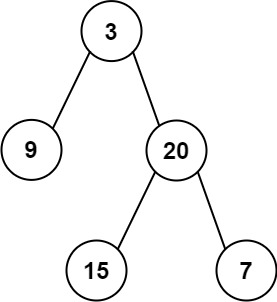
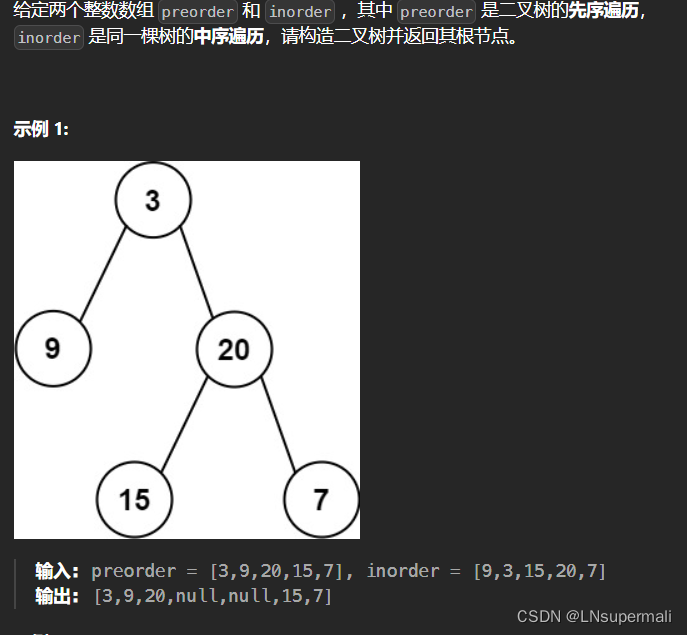
题目来源

力扣每日一题；题序：105

我的题解

方法一 递归

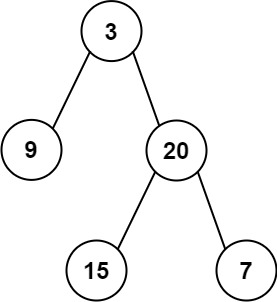
• 前序特点：[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
• 中序特点：[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
  只要在中序遍历中定位到根节点，那么就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。
  这样以来，就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

时间复杂度：O($n^2$) 。除了遍历节点，还需要扫描整个中序遍历的结果并找出根节点
空间复杂度：O(n)

public TreeNode buildTree(int[] preorder, int[] inorder) {
    return createTree(preorder,inorder,0,preorder.length-1,0,inorder.length-1);
}
// mid 根所在的位置
// pR 对应前序结束的位置
// iL 对应中序开始的位置
// iR 对应中序结束的位置
public TreeNode createTree(int[] preorder,int[] inorder,int mid,int pR,int iL,int iR){
    if(mid>pR||iL>iR)
        return null;
    int val=preorder[mid];
    TreeNode root=new TreeNode(val);
    int index=find(inorder,val,iL,iR);
    // 左子树的节点数量
    int left=index-iL;
    // 右子树的节点数量
    int right=iR-index;
// 构建左子树需要的前序序列和中序序列  pre[mid,mid+left]  in[iL,index-1]   root.left=createTree(preorder,inorder,mid+1,mid+left,iL,index-1);
// 构建右子树需要的前序序列和中序序列  pre[mid+left+1,pR]  in[index+1,iR]     root.right=createTree(preorder,inorder,mid+left+1,pR,index+1,iR);
    return root;
}
//在中序序列中找寻与前序对应的值val所在的位置
public int find(int[] inorder,int val,int iL,int iR){
    int index=iL;
    for(int i=iL;i<=iR;i++){
        if(inorder[i]==val){
            index=i;
        }
    }
    return index;
}

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，这样做需要频繁扫描，时间复杂度较高。可以考虑使用哈希表来帮助快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，就只需要 O(1)的时间对根节点进行定位了。

//哈希表优化版本
public TreeNode buildTree(int[] preorder, int[] inorder) {
    Map<Integer,Integer> map=new HashMap<>();
    //只需要遍历一次
    for(int i=0;i<inorder.length;i++){
        map.put(inorder[i],i);
    }
    return createTree(preorder,inorder,0,preorder.length-1,0,inorder.length-1,map);
}
public TreeNode createTree(int[] preorder,int[] inorder,int mid,int pR,int iL,int iR,Map<Integer,Integer> map){
    if(mid>pR||iL>iR)
        return null;
    int val=preorder[mid];
    TreeNode root=new TreeNode(val);
    //直接根据哈希表确定位置
    int index=map.get(val);
    int left=index-iL;
    int right=iR-index;
    root.left=createTree(preorder,inorder,mid+1,mid+left,iL,index-1,map);
    root.right=createTree(preorder,inorder,mid+left+1,pR,index+1,iR,map);
    return root;
}

方法二 迭代

看官方题解吧，没怎么弄明白

有任何问题，欢迎评论区交流，欢迎评论区提供其它解题思路（代码），也可以点个赞支持一下作者哈😄~