einsum 是 Einstein summation 的缩写,来源于爱因斯坦求和约定(Einstein summation convention)。这是物理学家阿尔伯特·爱因斯坦引入的一种简便记号,用于描述张量运算,特别是涉及多维数组的运算。
示例1:矩阵乘法
矩阵乘法 C=AB
A = torch.randn(2, 3)
B = torch.randn(3, 4)
C = torch.einsum('ik,kj->ij', A, B)
print(C.size()) # 输出: torch.Size([2, 4])
这里,'ik,kj->ij' 的含义是:
A的形状为(2, 3),对应ik,i和k分别表示第一个和第二个维度。B的形状为(3, 4),对应kj,k和j分别表示第一个和第二个维度。->ij表示输出张量的模式,结果为(2, 4)。
示例2:向量点积
向量点积 c=a⋅b
a = torch.randn(3)
b = torch.randn(3)
c = torch.einsum('i,i->', a, b)
print(c.size()) # 输出: torch.Size([])
这里,'i,i->' 的含义是:
a和b都是向量,对应模式i。->后面为空,表示结果是一个标量。
示例3:批量矩阵乘法
批量矩阵乘法
A = torch.randn(10, 2, 3)
B = torch.randn(10, 3, 4)
C = torch.einsum('bij,bjk->bik', A, B)
print(C.size()) # 输出: torch.Size([10, 2, 4])
这里,'bij,bjk->bik' 的含义是:
A的形状为(10, 2, 3),对应bij,b表示批次维度,i和j分别表示矩阵的行和列。B的形状为(10, 3, 4),对应bjk,b表示批次维度,j和k分别表示矩阵的行和列。->bik表示输出张量的模式,结果为(10, 2, 4)。
示例4:逐元素相乘(哈达玛积)A.B或A × B
A = torch.randn(3, 4)
B = torch.randn(3, 4)
C = torch.einsum('ij,ij->ij', A, B)
print(C.size()) # 输出: torch.Size([3, 4])
'ij,ij->ij' 表示:
A和B都是形状为[3, 4]的矩阵,用ij表示。- 结果
C也是形状为[3, 4]的矩阵。 - 没有重复索引,所以不进行求和。

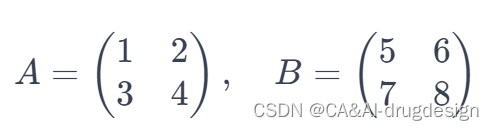

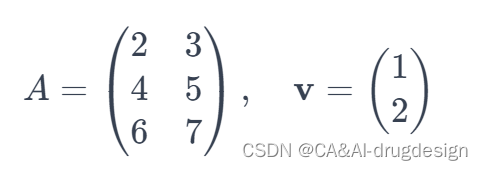
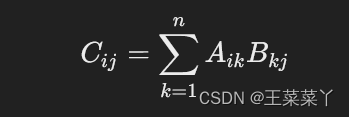























![[C++] 在VS code中打开VS studio的cpp文件并调试运行(弹出独立窗口)](https://img-blog.csdnimg.cn/img_convert/230d6dfb13f74cb7b60e4fa801a1f385.webp?x-oss-process=image/format,png)
![[Bug] Error: cannot import name ‘ALBERT_PRETRAINED_MODEL_ARCHIVE_LIST‘](https://img-blog.csdnimg.cn/direct/c9280967650a478f9728a0dfb0a820fd.png)
![[经验] 油汀取暖器怎么用-油汀取暖器使用方法详解 #媒体#学习方法](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Fwww.hao123rr.com%2Fzb_users%2Fcache%2Fly_autoimg%2F%25E6%25B2%25B9%25E6%25B1%2580%25E5%258F%2596%25E6%259A%2596%25E5%2599%25A8%25E6%2580%258E%25E4%25B9%2588%25E7%2594%25A8-%25E6%25B2%25B9%25E6%25B1%2580%25E5%258F%2596%25E6%259A%2596%25E5%2599%25A8%25E4%25BD%25BF%25E7%2594%25A8%25E6%2596%25B9%25E6%25B3%2595%25E8%25AF%25A6%25E8%25A7%25A3.jpg&pos_id=FpgvuF92)