一、经验总结
优先级队列(堆),常用于在集合中筛选最值或解决TopK问题。
提示:对于固定序列的TopK问题,最优解决方案是快速选择算法,时间复杂度为O(N)比堆算法O(NlogK)更优;而对于动态维护数据流中的TopK,最优解决方案是堆算法,每次添加数据后筛选,时间复杂度为O(logK)比快速选择算法O(N)更优;
优先级队列如何解决TopK问题?
- 创建一个大小为K的堆
- 循环
- 将数组中的元素依次进堆
- 判断堆中的元素个数是否大于K,如果大于K就pop弹出堆顶元素
- 将数组中的所有元素全部筛选一遍后,堆中剩余的K个元素就是最大(小)的K个元素
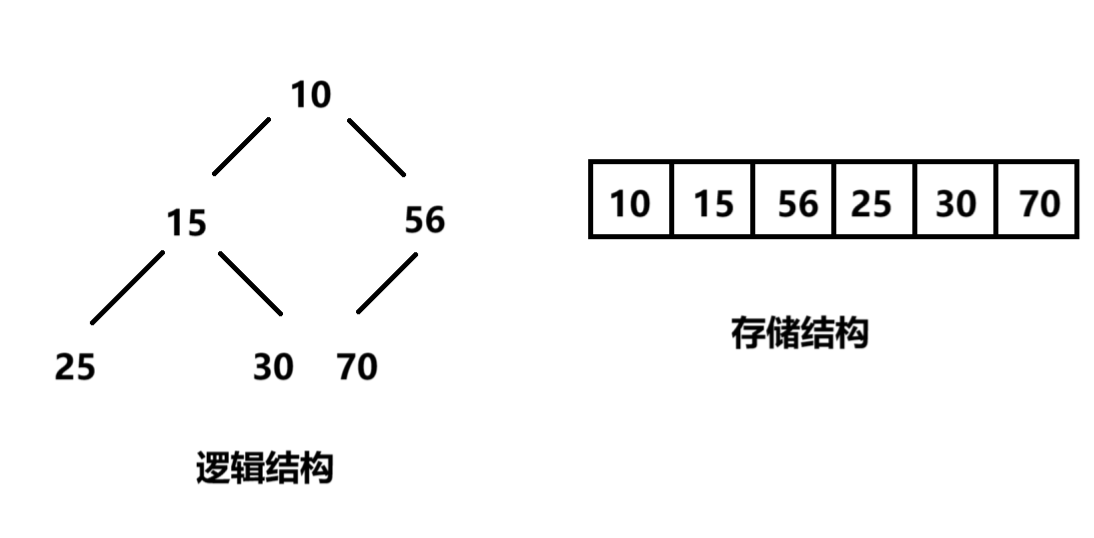
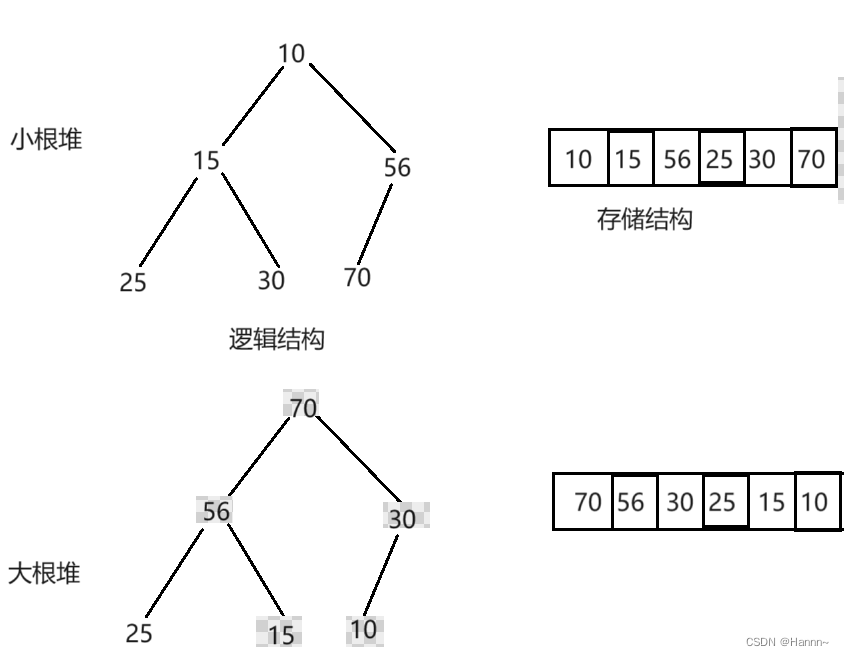
TopK问题选用大根堆还是小根堆?
- 如果要选出最大的K个数,就选用小根堆;
- 如果要选出最小的K个数,就选用大根堆;
利用大小堆维护数据流中的中位数
- 创建一个大堆left用于存储数据流的前一半(升序),一个小堆right用于存储后一半
- 控制left的元素个数m和right的元素个数n满足:m==n或m==n+1
- 数据流的中位数:当m==n时,mid=(left.top()+right.top())/2;当m==n+1时,mid=left.top();
- 新增元素:将新元素与left.top()(或right.top())比较,决定加入left还是right。完成插入后,记得调整两个堆的元素个数使其满足规则。
二、相关编程题
2.1 最后一块石头的重量
题目链接
1046. 最后一块石头的重量 - 力扣(LeetCode)
题目描述

算法原理
利用堆结构筛选最大值
编写代码
class Solution {
public:
int lastStoneWeight(vector<int>& stones) {
priority_queue<int> heap;
for(auto e : stones) heap.push(e);
while(heap.size() >= 2)
{
int s1 = heap.top();
heap.pop();
int s2 = heap.top();
heap.pop();
if(s1 > s2) heap.push(s1-s2);
}
if(heap.size() == 0) return 0;
else return heap.top();
}
};
2.2 数据流中的第 K 大元素
题目链接
703. 数据流中的第 K 大元素 - 力扣(LeetCode)
题目描述

算法原理

这道题更适合使用堆解决,因为add函数插入一个数字后返回当前数据中的第K大的元素,如果使用快速选则算法,复杂度为O(N);而使用堆算法,复杂度为O(logK)
编写代码
class KthLargest {
priority_queue<int, vector<int>, greater<int>> _heap;
int _k;
public:
KthLargest(int k, vector<int>& nums) {
_k = k;
for(auto e : nums) add(e);
}
int add(int val) {
_heap.push(val);
if(_heap.size() > _k)
_heap.pop();
return _heap.top();
}
};
2.3 前K个高频单词
题目链接
题目描述

算法原理

编写代码
class Solution {
typedef pair<string, int> PSI;
struct Cmp{
bool operator()(const PSI &left, const PSI &right)
{
if(left.second != right.second) //出现频次不同,选出高频单词,按照小根堆的方式排列
return left.second > right.second;
else
return left.first < right.first; //出现频次相同,按字典序排序,按照大根堆的方式排列
}
};
public:
vector<string> topKFrequent(vector<string>& words, int k) {
unordered_map<string, int> hash;
priority_queue<PSI, vector<PSI>, Cmp> heap;
vector<string> ret(k);
//统计所有单词的出现频次
for(auto &str:words)
{
++hash[str];
}
//用一个大小为k的堆筛选TopK
for(auto &psi:hash)
{
heap.push(psi);
if(heap.size() > k)
heap.pop();
}
//将结果倒着放入数组
for(int i = k-1; i >= 0; --i)
{
ret[i] = heap.top().first;
heap.pop();
}
return ret;
}
};
2.4 数据流的中位数
题目链接
题目描述

算法原理

编写代码
class MedianFinder {
priority_queue<int> left; //大根堆
priority_queue<int, vector<int>, greater<int>> right; //小根堆
public:
MedianFinder() {}
void addNum(int num) {
if(left.size() > right.size()) //m > n
{
int x = left.top();
if(num <= x)
{
left.push(num);
left.pop();
right.push(x);
}
else
{
right.push(num);
}
}
else //m == n
{
int y = right.empty()? 0:right.top();
if(right.empty() || num < y)
{
left.push(num);
}
else
{
right.push(num);
right.pop();
left.push(y);
}
}
}
double findMedian() {
if(left.size() > right.size()) //m > n
return (double)left.top();
else //m == n
return (left.top()+right.top())/2.0;
}
};