leetcode77组合——经典回溯算法

本文主要讲解组合的要点与细节，以及回溯算法的解题步骤，按照步骤思考更方便理解 

c++和java代码如下，末尾

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

 具体要点：

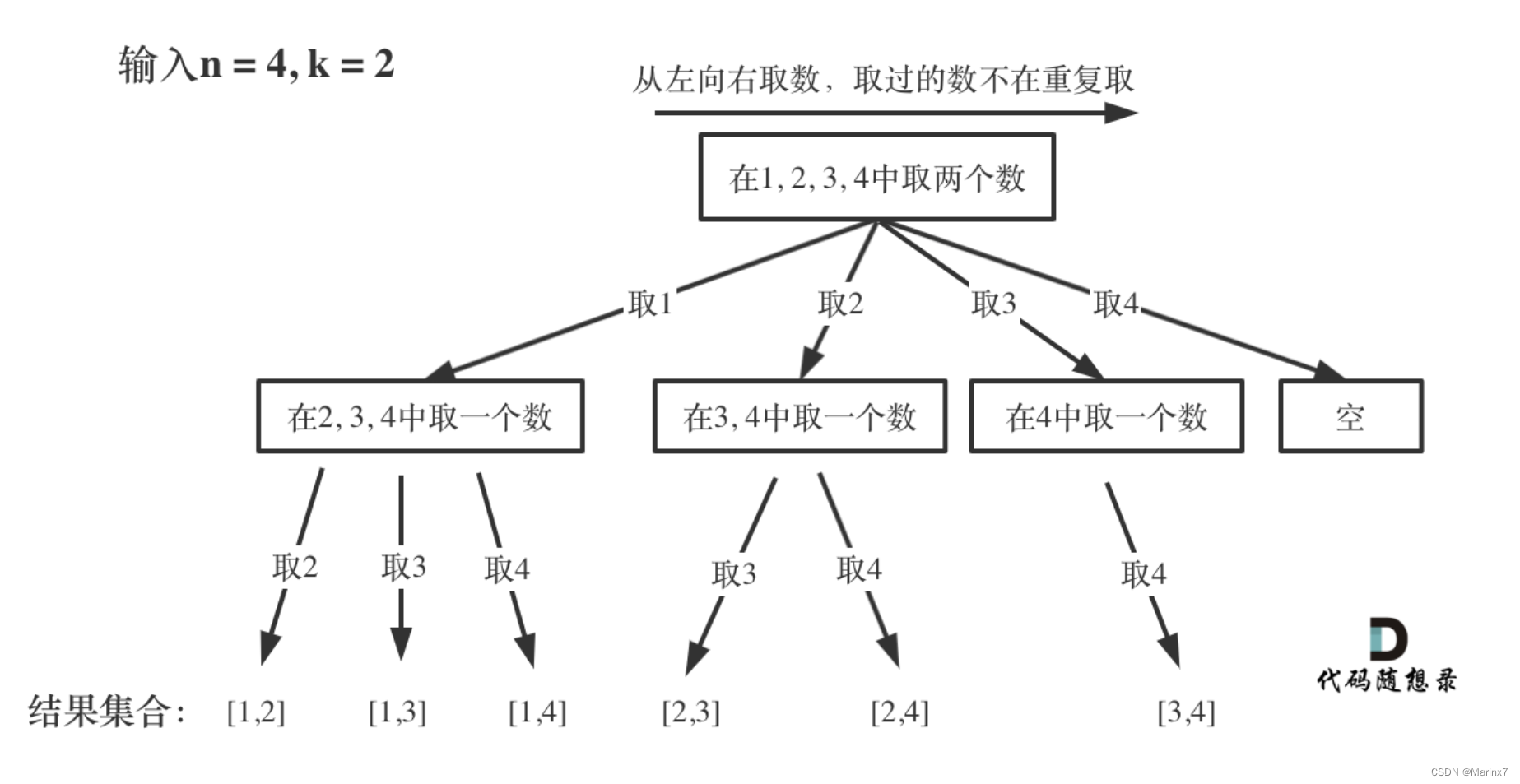
1. 首先，这道题的暴力解法是k层for循环，遍历所有的情况。但是这样子时间复杂度会很高。所以对于这类排列组合的问题，通常我们使用回溯算法来进行遍历，可以花一分钟参考回溯的前言概述。

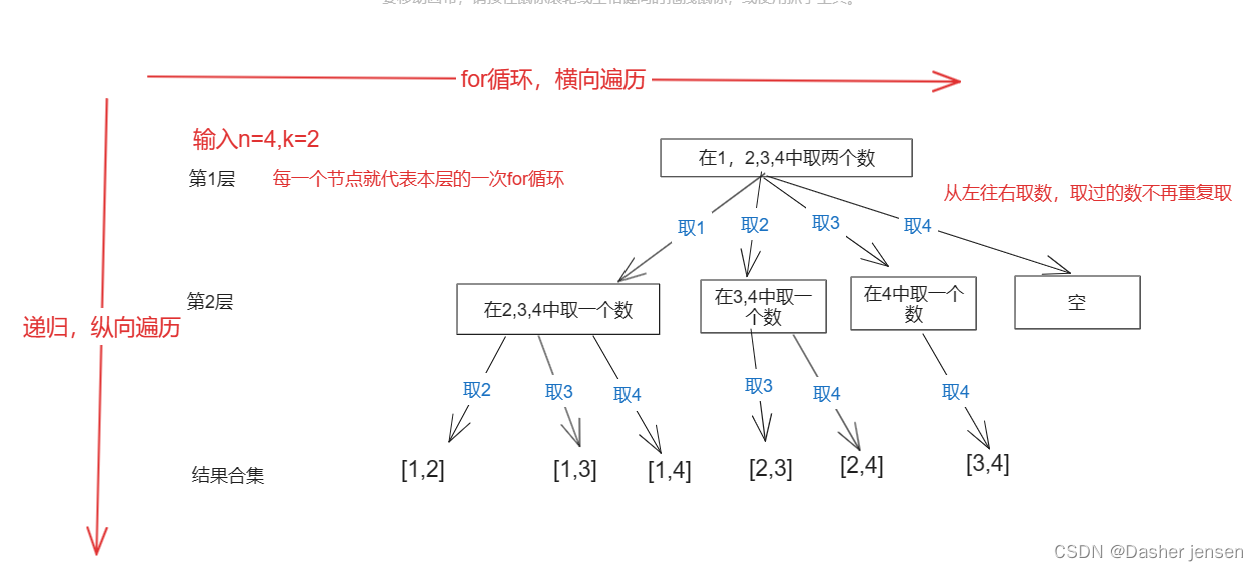
2. 然后让我们来回顾一下回溯，回溯本质是一个树结构通常是由两个结构组成：for+递归。

        其中，for用来表示树的宽度，遍历每层的集合元素集，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

        递归用来表示树的深度

3. 对于本题要求，我们需要先创建两个数组，一个用来存放最终的结果，一个用来存放过程中每次的结果

vector<vector<int>> res; //用来存放最终的结果
vector<int> temp; //用来存放过程中每次的结果

 4. 接着我们就可以考虑回溯算法的实现，具体包括两部分：for循环+递归

首先，我们来考虑递归，说到递归，就要思考递归三要素：

• 递归函数参数与返回值
• 终止条件
• 单层递归逻辑

返回值：由于我们是直接操作数组，不像二叉树一样需要返回节点，所以递归的返回值是void

参数：回溯算法中的递归参数较多，我们在写代码过程中慢慢添加

终止条件：也就是我们收集结果的条件，当我们的temp存放的数量等于k时，就需要收集结果了

单层递归逻辑：添加当前元素a到temp中——a向下递归——移除刚才添加的元素a

其次，让我们考虑一下for循环的细节

        for循环的起始值应该是什么呢？

        这个细节是回溯中重要的点，因为本题是“组合”，所以不需要顺序，即{1，2}和{2，1}是一个意思，只保留一个，所以下一层递归时，起始值就+1，从而达到去重的目的。

    void backtracing(int n, int k,
                    vector<vector<int>>& res, vector<int> temp,
                    int start
        ) {
        //终止条件
        if (temp.size() == k) {//收集结果
            res.push_back(temp);
            return;
        }
        for (int i = start; i <= n; ++i) {
            temp.push_back(i);//添加当前元素
            backtracing(n, k, res, temp, i + 1);//相下递归，起始值+1
            temp.pop_back();//删除刚才添加的元素，实现回溯
        }
        return;
    }

以上就是回溯的整体逻辑，让我们总结一下重要的细节：

• 递归的返回值
• 递归的终止条件
• for循环的起始值

在回溯过程中大家重点思考一下这几个细节点，有助于我们更好的实现代码

如果觉得我的讲解有一点帮助，十分感谢您的喜欢。

c++代码：

#include<bits/stdc++.h>
using namespace std;

class Solution {
public:
    vector<vector<int>> combine(int n, int k) {
        //组合，不考虑顺序
        vector<vector<int>> res;
        vector<int> temp;
        backtracing(n, k, res, temp, 1);
        return res;
    }
    void backtracing(int n, int k,
                    vector<vector<int>>& res, vector<int> temp,
                    int start
        ) {
        //终止条件
        if (temp.size() == k) {//收集结果
            res.push_back(temp);
            return;
        }
        for (int i = start; i <= n; ++i) {
            temp.push_back(i);//添加当前元素
            backtracing(n, k, res, temp, i + 1);//相下递归
            temp.pop_back();//删除刚才添加的元素，实现回溯
        }
        return;
    }
        
};

java代码

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        List<Integer> temp = new ArrayList<>();
        backtracking(n, k, res, temp, 1);
        return res;

    }

    public void backtracking(int n, int k, List<List<Integer>> res, List<Integer> temp, int start) {
        //终止条件
        if (temp.size() == k) {
            res.add(new ArrayList<>(temp));
            return;
        }
        for (int i = start; i <= n; i++) {
            temp.add(i);
            backtracking(n, k, res, temp, i + 1);
            temp.remove(temp.size() - 1);
        }
        return;
    }
}