子集与全排列问题（力扣78,90,46,47）

系列文章目录

子集和全排列问题与下面的组合都是属于回溯方法里的，相信结合前两期，再看这篇笔记，更有助于大家对本系列的理解

文章目录

系列文章目录
题目
子集
子集II
全排列
全排列II
总结

题目

Problem: 78. 子集
Problem: 90. 子集 II
Problem: 46. 全排列
Problem: 47. 全排列 II

子集II与全排列II都只是在前面的基础上加了题目所给的nums数组里的元素可重复这个条件
子集问题：
给你一个整数数组 nums ，数组中的元素互不相同。返回该数组所有可能的
子集（幂集）。解集不能包含重复的子集。你可以按任意顺序返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

全排列问题：
给定一个不含重复数字的数组 nums ，返回其所有可能的全排列。你可以按任意顺序返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

子集

一、思路

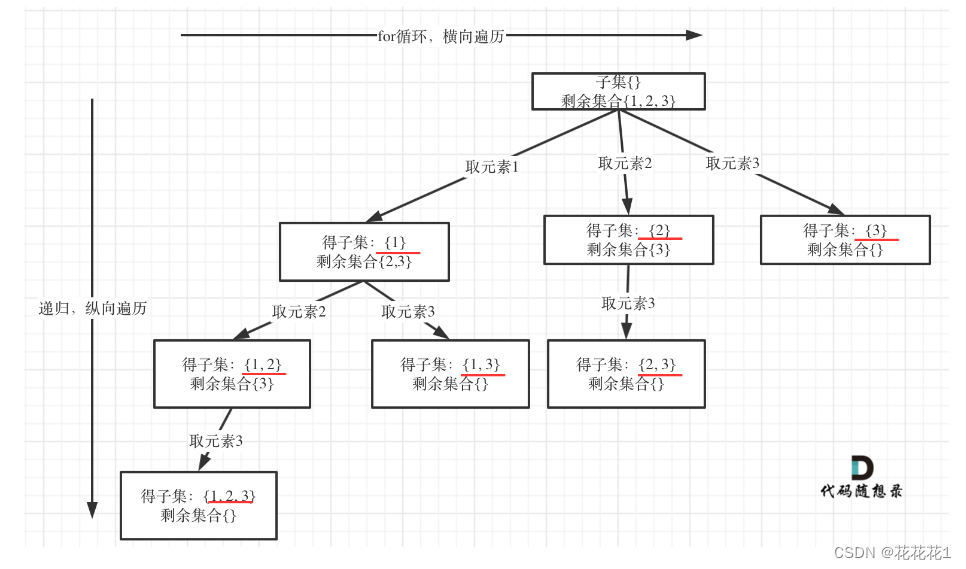
与组合和组合总和问题不同的是每遍历到一个树的结点，都要把结果加入到result结果集里面，而不是到叶子结点时，才收集结果

例：从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合
在这里插入图片描述

二、解题方法

回溯三部曲

递归函数的返回值以及参数：
参数为startIndex和nums整数数组

 public void backTracking(int[] nums,int startIndex)

回溯函数终止条件：
到叶子结点时就退出递归，去遍历其它路径上的结果

if(startIndex >= nums.length) {
            return;
        }

单层搜索的过程：
每遍历一次都把元素添加到路径path中，递归回溯，每次递归startIndex都从后一位递归，否则会造成重复的组合。

for(int i = startIndex;i<nums.length;i++) {
            path.add(nums[i]);
            backTracking(nums,i+1);
            path.removeLast();
        }

在每层递归函数里，都要把当前路径添加到result结果集中，要写在终止条件之前，否则退出之后，当前结果还没有保存就回溯其它路径上的结果了。

result.add(new ArrayList<>(path));

优化：在这里其实可以省略掉终止条件，因为就算遍历超过叶子结点了，不满足for循环的条件里，for循环里面也不会执行，就直接return了。

三、Code

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> subsets(int[] nums) {
        backTracking(nums,0);
        return result;
    }

    public void backTracking(int[] nums,int startIndex) {
        result.add(new ArrayList<>(path));
        if(startIndex >= nums.length) {
            return;
        }
        for(int i = startIndex;i<nums.length;i++) {
            path.add(nums[i]);
            backTracking(nums,i+1);
            path.removeLast();
        }
    }
}

子集II

一、思路

这道题与子集I的区别在于题目给的数组元素可重复，这就要对组合结果去重，与组合总和II是相同的套路，都是先排序之后，再判断前面同一层是否出现了相同的访问过的元素，如果出现了则直接跳过这次循环

在这里插入图片描述

二、解题方法

与上面的子集问题I多了先对nums数组进行排序，在for循环内对横向遍历去重，去重的方法和组合总和II是一样的有以下两种：

used数组:
如果前面的元素和当前元素相同，并且i>0,前面的元素没有使用过，说明不是同一条路径下使用过的的元素，而是同一层内的

if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
                continue;
            }

startIndex:
如果前面的元素和当前元素相同，并且startIndex已经不是第一个开始遍历的，则直接跳过这次循环

if(i > startIndex && nums[i] == nums[i-1]){
                continue;
            }

三、Code

used数组

class Solution {
   List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
   LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
   boolean[] used;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        used = new boolean[nums.length];
        subsetsWithDupHelper(nums, 0);
        return result;
    }
    
    private void subsetsWithDupHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));

        if (startIndex >= nums.length){
            return;
        }

        for (int i = startIndex; i < nums.length; i++){
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
                continue;
            }

            path.add(nums[i]);
            used[i] = true;
            subsetsWithDupHelper(nums, i + 1);
            path.removeLast();
            used[i] = false;
        }
    }
}

startIndex

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backTracking(nums,0);
        return result;
    }

    public void backTracking(int[] nums,int startIndex) {
        result.add(new ArrayList<>(path));

        if(startIndex >= nums.length) {
            return;
        }

        for(int i = startIndex;i<nums.length;i++) {
            if(i > startIndex && nums[i] == nums[i-1]){
                continue;
            }
            path.add(nums[i]);
            backTracking(nums,i + 1);
            path.removeLast();
        }
    }
}

全排列

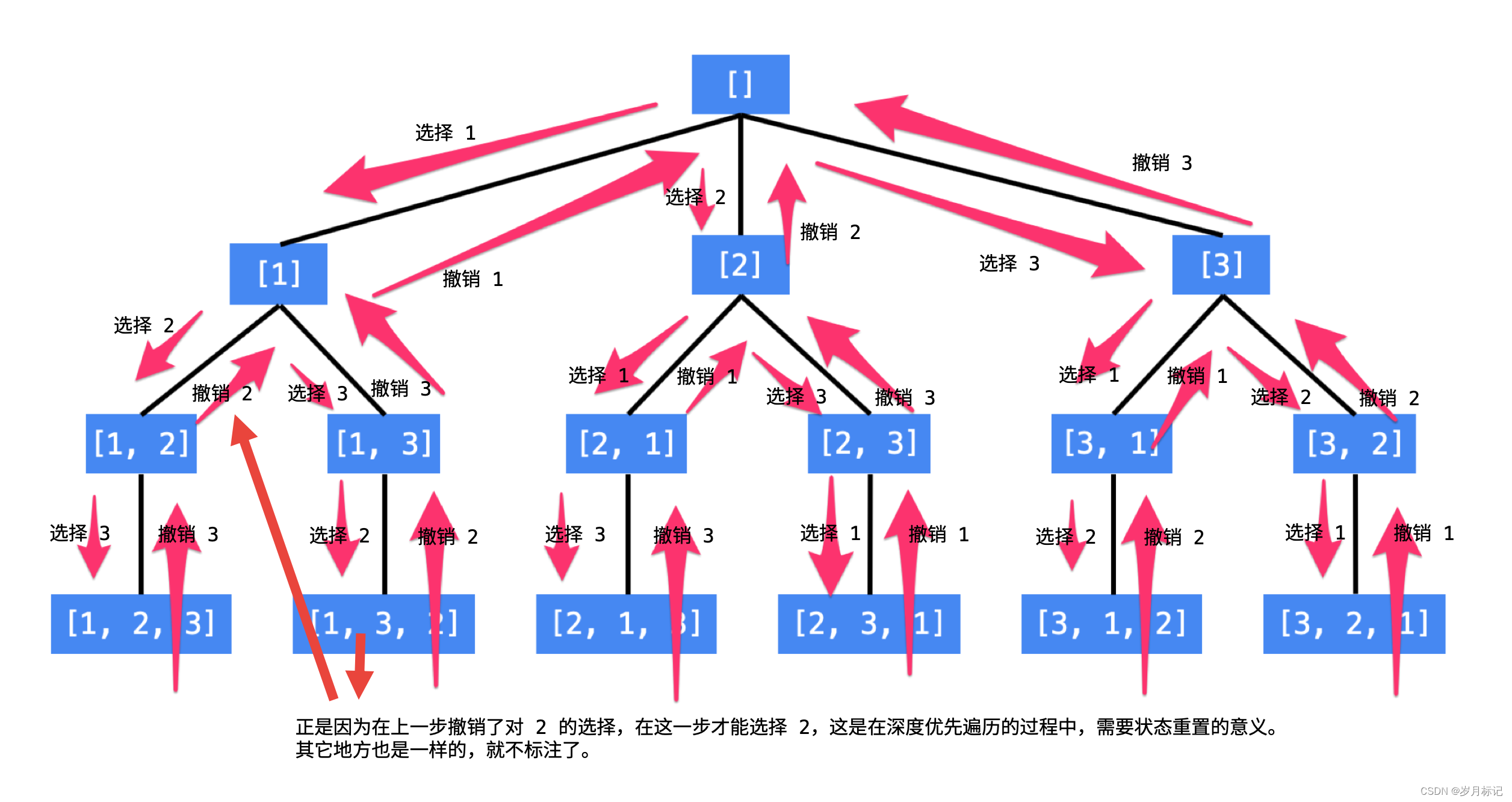
一、思路

全排列的话[1,2]和[2,1]是不一样的排列，与组合不同，排列要求顺序，所以不需要使用startIndex，只需判断元素是否使用过，如果不判断同一条路径path上的结果是否使用过的话，会一直重复遍历同一个元素，例如：整数数组为[1,2,3,4]，那么就会一直遍历1，有两种判断的办法：
一是used数组，二是path.contains(nums[i])，

二、解题方法

used数组

递归函数的返回值以及参数：
参数为nums整数数组，创建一个used布尔类型的数组，长度为nums数组的长度

private void permuteHelper(int[] nums)

回溯函数终止条件：
到达叶子结点时，就把结果添加到结果集里，退出递归

if (path.size() == nums.length){
    result.add(new ArrayList<>(path));
    return;
}

单层搜索的过程：
for循环从第一个元素开始遍历，used数组判断如果为true，则跳过这次循环，找数组里下一个元素，没有使用过的话，就把元素添加到path里，并让used数组为true，递归调用，回溯撤销元素，让used数组为false

for (int i = 0; i < nums.length; i++){
            if (used[i]){//使用过该元素
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }

path.contains(nums[i])：
只要把for循环内的判断used数组改为path.contains(nums[i])即可，判断path有没有添加过该元素

if(path.contains(nums[i])){
    continue;
}

三、Code

used数组

class Solution {
    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums){
        if (path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++){
            if (used[i]){//使用过该元素
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

path.contains(nums[i])

class Solution {
    List<List<Integer>> result = new ArrayList<>();
	LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        backTracking(nums);
        return result;
    }

    public void backTracking (int[] nums) {
        if(path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i = 0;i<nums.length;i++) {
            if(path.contains(nums[i])){
                continue;
            }
            path.add(nums[i]);
            backTracking(nums);
            path.removeLast();
        }
    }
}

全排列II

一、思路

此题比上面的全排列I 只多了一个数组元素可重复，与组合总和II、子集II是相同的都要进行先排序再去重，用到used数组判断同一层是否使用过，使用过的话，直接跳过这次循环
在这里插入图片描述

二、解题方法

与全排列I使用used数组的回溯三部曲大致相同，仅仅多了先对数组进行排序，随后判断同一层是否使用过，这个与组合总和II，子集II的通过used数组判断去重是一样的，在此省略

三、Code

class Solution {
    List<List<Integer>> result = new ArrayList<>();
	LinkedList<Integer> path = new LinkedList<>();
    boolean[] used;

    public List<List<Integer>> permuteUnique(int[] nums) {
        if (nums.length == 0){
            return result;
        }
        used = new boolean[nums.length];
        Arrays.sort(nums);
        backTracking(nums);
        return result;
    }

    private void backTracking(int[] nums){
        if (path.size() == nums.length){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = 0; i < nums.length; i++){
            // 同一层用过直接跳过去重
            if(i>0 && nums[i] == nums[i-1] && used[i-1] == false){
                continue;
            }

            // 同一条结果路径上没有使用过
            if (used[i] == false){
                used[i] = true;
                path.add(nums[i]);
                backTracking(nums);
                path.removeLast();
                used[i] = false;
            }
            
        }
    }
}