167.木棒
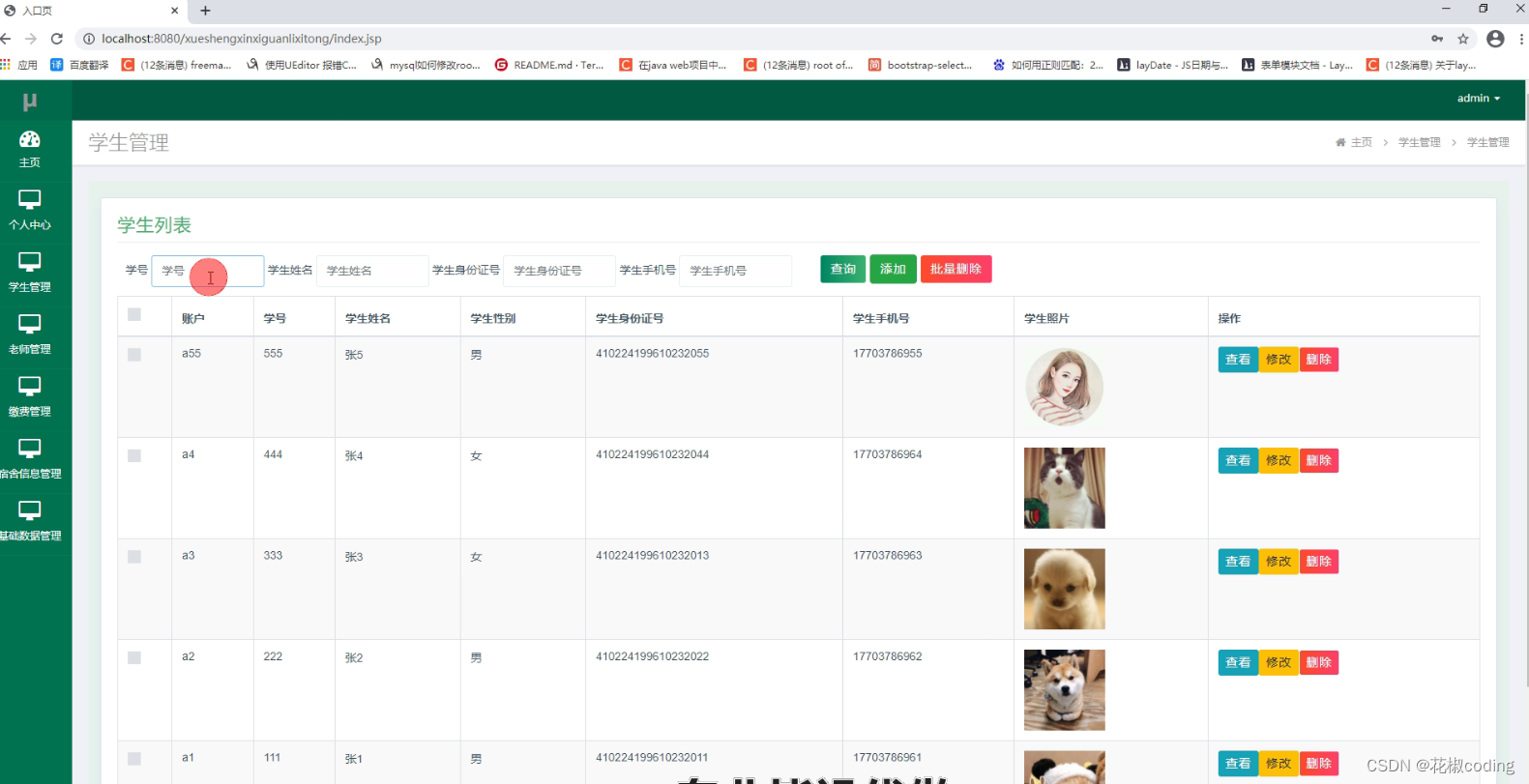
| 167. 木棒 - AcWing题库 |
|---|
| 难度:中等 |
| 时/空限制:1s / 64MB |
| 总通过数:17542 |
| 总尝试数:44639 |
| 来源: 《算法竞赛进阶指南》UVA307 |
| 算法标签 搜索DFS剪枝 |
题目内容
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
输入格式
输入包含多组数据,每组数据包括两行。
第一行是一个不超过 64 的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
输出格式
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
数据范围
数据保证每一节木棍的长度均不大于 50。
输入样例:
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
输出样例:
6
5
题目详解
给我们N个不超过50的数,每个数表示每根木棍的长度,把这些木棍拼成若干个长度相等的大木棍的话,每根大木棍的长度的最小值是多少
用暴力搜索去做
暴搜顺序
- 从小到大枚举一下最终答案的长度,从小到大找到的第一个成立的长度就一定是答案
- 长度需要满足条件,每个木棍的长度成立的话,一定是总和的约数,所以需要加一些剪枝
- 从前往后一根一根去拼,直到把所有的木棍用为止,从前往后依次去拼每次长度为最终长度的木棍
如果可以把所有木棍都用完的话,答案就是此时枚举的最终长度
没有必要用二分,当最终长度很小的时候,很快会发现是无解的,所以从小到大枚举的时候,计算量是倍增的,这个时候二分是没有什么意义的,因为下一集的计算量远远大于前面计算量的总和
优化
优化搜索顺序
递归的时候是一个深度优先搜索树,优先选择深度短的来搜,因为深度越短越容易尽早发现剪枝,尽可能地可以剪掉一些无用状态
这样的话,什么样的顺序去选可以样深度比较浅?
优先选择比较长的小木棍,把这个坑占好了之后,剩余的空间选择的深度就不会太大,所以搜索顺序就是从大到小去枚举
这样可以在搜索的时候尽可能更早地触发剪枝条件排除一些冗余的状态
拼一根木棍的时候,1,3,5、3,1,5、5,1,3这三种都是一样的,有可能会因为顺序产生一些等效冗余的方案,因此在搜的时候可以人为定一个状态。这样每一个顺序只取一个,比如这里可以排除3!个冗余方案
要求每一个长木棍内部的小木棍的编号从小到大递增
常见的优化方式,在搜方案的时候不考虑顺序,把一种排列的方案变成组合的方案,可行性剪枝
比如现在已经拼出了一些长度为最终长度的木棍,当前在拼下一节长度为当前枚举的长度的木棍,下一根木棍是第i根木棍,把后面的情况暴搜完之后,发现它无解,就要触发可行性剪枝
可行性剪枝有三类
1.
如果当前的木棍拼到这,失败之后,就要跳过所有长度跟当前木棍相等的其他木棍
证明
比如当前第i根木棍拿过来试了一下不成立,假设接下来的第j根木棍跟第i根木棍的长度是一样的,
换成j之后,是成立的话,必然存在一个方案,把所有长度为当前枚举最终长度的木棍都可以拼出来,由于所有的木棍都会被用掉,所以第i根木棍一定会被用,设第i根木棍在后面的某个位置,因为j和i长度是一样的,所以把i和j交换,仍然是一个方案,把j交换过去之后,在按编号从小到大排序,发现就可以构造一个把i放到当前位置的方案,就与i放到当前位置矛盾
2.
假设现在已经拼了一些长度为当前枚举的最终长度的长木棍,在拼下一根新木棍的时候,从前往后找到第一根没有用过的小木棍,把这根木棍放到当前的最新的要拼的这棍木棍的第一个,放完之后如果无解的话,则当前方案一定无解
证明
i是编号从小到大,第一根没有用过的木棍,如果i作为当前新木棍的第一根不成立的话,
如果最后存在一个方案,可以把这个方案设出来,i就不能作为当前长木棍里面的木棍了,就只能作为其余木棍里面的木棍,由于i是当前第一根没有被用过的木棍,每一根长木棍内部的短木棍的编号都是递增的,所以i就必然在未来的某一根长木棍里面是第一根,如果把这两个方案交换一下,就可以构造出来一个当前第i根木棍作为当前长木棍第一根的一个方案,就矛盾了
3.
在拼某一根长木棍的时候,如果把第i根木棍放到最后一个位置,刚好可以把当前的木棍凑满的话,但是又无解,
把当前第i根木棍凑到最后一个位置的话,整个木棍的长度满足条件,等于当前枚举的最终长度,但是后面无解,后面剩余的木棍拼不好它,这种情况下也无解
若当前小木棍作为最后一根加上后,当前的长木棍已经满足要求了,则一定无解
证明
假设把第i根木棍放到了当前的位置,刚好凑了一根长度为最终长度的长木棍,但是剩余的木棍是无解的,无法凑成长度为枚举最终长度的长木棍,它是无解的
如果有解的话,这里必然是用多余一根来凑出来, 假设有两根把i的位置凑出来了,由于当前方案是一组解,所以i一定会被用到,i就会出现在未来的某一根长木棍里,把i和这两根交换一下,交换以后,这两根还要按照编号从小到大排序,这样仍然是一组解,而且i是作为了当前最后一根的位置,就矛盾了
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 70;
int n;
int w[N]; //用w表示每根木棍的长度
bool st[N]; //表示每根木棍有没有被用过
int sum; //表示当前木棍的总长度
int len; //表示当前枚举的长度
//当前枚举到第几根长木棍,当前正在拼的长木棍的长度,当前长木棍内小木棍的下标
bool dfs(int u, int cur, int start)
{
//判断一下,如果把所有的小木棍都拼成长木棍的话
if (u * len == sum)
return true;
//如果当前的长木棍已经拼好了,就枚举下一根木棍
if (cur == len)
return dfs(u + 1, 0, 0);
for (int i = start; i < n; i ++)
{
//如果当前的小木棍已经被用过了
if (st[i])
continue;
//判断当前木棍能不能拿来用
if (cur + w[i] <= len)
{
st[i] = true;
//如果用当前木棍能凑到方案的话
if (dfs (u, cur + w[i], i + 1))
return true;
st[i] = false;
}
//第2,3个剪枝
//如果发现当前正在拼一根新的长木棍,或者是当前的最后一根
if (!cur || cur + w[i] == len)
return false;
//第1个剪枝
int j = i + 1;
while (j < n && w[i] == w[j])
j ++;
i = j - 1;
}
//如果无解
return false;
}
int main()
{
//因为有多组数据,每次读入一个n,判断n是不是0
while (cin >> n, n)
{
//清空一下
sum = len = 0;
//从前往后依次读取每一根长木棍
for (int i = 0; i < n; i ++)
{
cin >> w[i];
//更新一下总和
sum += w[i];
//最小的长度一定大于等于对短的一根的长度
len = max(len, w[i]);
}
//排序
sort (w, w + n, greater<int>());
//先清空一下,表示每一根木棍都没有被用过
memset(st, 0, sizeof st);
//从小到大取枚举
while (true)
{
//每次判断一下当前的len成不成立,能整除并且能搜到方案的话,就成立
if (sum % len == 0 && dfs(0, 0, 0))
{
//就把len输出
cout << len << endl;
break;
}
len ++;
}
}
return 0;
}